Vijaya Sree

Browse chapter 1 go math grade 7 resources on our Go Math Answer Key. So, the students who are looking for chapter 1 pdf can Download Go Math Grade 7 Answer Key here. You can enhance your skills by practicing the problems from Go Math Grade 7 Answer Key Chapter Adding and Subtracting Integers.

Go Math Grade 7 Answer Key Chapter 1 Adding and Subtracting Integers

Check out the topics of Grade 7 chapter 1 before you start your preparation for exams. This chapter contains topics like Adding Integers with the Same Sign, Different sign, Subtracting Integers, Applying Addition and Subtraction of Integers, etc. Make use of the below links and solve the questions.

Chapter 1 – Adding Integers with the Same Sign

• Adding Integers with the Same Sign – Guided Practice – Page No. 10
• Adding Integers with the Same Sign – Independent Practice – Page No. 11
• Adding Integers with the Same Sign – Page No. 12

Chapter 1 – Adding Integers with Different Signs

• Adding Integers with Different Signs – Guided Practice – Page No. 16
• Adding Integers with Different Signs – Independent Practice – Page No. 17
• Adding Integers with Different Signs – Page No. 18

Chapter 1 – Subtracting Integers

• Subtracting Integers – Guided Practice – Page No. 22
• Subtracting Integers – Independent Practice – Page No. 23
• Subtracting Integers – Page No. 24

Chapter 1 – Applying Addition and Subtraction of Integers

• Applying Addition and Subtraction of Integers – Guided Practice – Page No. 28
• Applying Addition and Subtraction of Integers – Independent Practice – Page No. 29

Chapter 1 – MODULE 1

• Module Quiz – Ready to Go On – Page No. 31
• Module Quiz – MODULE 1 MIXED REVIEW – Page No. 32
• MODULE 1 MIXED REVIEW
• Module 1 Review – Adding and Subtracting Integers – Page No. 103

Adding Integers with the Same Sign – Guided Practice – Page No. 10

Find each sum.

Question 1.
-5 + (-1)

a. How many counters are there?
_______ counters

Answer: 6

Explanation:
By seeing the above pictures we can say that there are 6 counters.

Question 1.
b. Do the counters represent positive or negative numbers?
____________

Answer: negative numbers

Explanation:
The counters are red so they represent negative numbers.

Question 1.
c. -5 + (-1) =
_______

Answer: -6

Explanation:
There are 6 counters so -5 + (-1) = – 6

Adding Integers with the Same Sign Worksheet Answers Question 2.
-2 + (-7)

a. How many counters are there?
_______ counters

Answer: 9

Explanation:
The above figure shows that there are 9 counters.

Question 2.
b. Do the counters represent positive or negative numbers?
____________

Answer: negative numbers

Explanation:
The counters are red so they represent the negative numbers.

Question 2.
c. -2 + (-7) =
_______

Answer: -9

Explanation:
There are 9 counters so -2 + (-7) = -9
The answer is -9.

Model each addition problem on the number line to find each sum.

Question 3.
-5 + (-2) =

_______

Answer: -7

Explanation:
Remember if the number being added is positive more number of units going to the right and if the number being added is negative more number of units to the left.
Since we are adding the negative number starting from -5, we move 2 units to the left. This results in -7.

Question 4.
-1 + (-3) =

_______

Answer: -4

Explanation:
Remember if the number being added is positive more number of units going to the right and if the number being added is negative more number of units to the left.
Since we are adding a negative number starting from -1, we move 3 units to left. This results in -4.

Question 5.
-3 + (-7) =

_______

Answer: -10

Explanation:
Remember if the number being added is positive more number of units going to the right and if the number being added is negative more number of units to the left.
Since we are adding a negative number starting from -3, we move 7 units to the left. This results in -10.

Adding Integers on a Number Line Worksheet Answer Key Question 6.
-4 + (-1) =

_______

Answer: -5

Explanation:
Remember if the number being added is positive more number of units going to the right and if the number being added is negative more number of units to the left.
Since we are adding a negative number starting from -4, we move 1 unit to the left. This results in -5.

Question 7.
-2 + (-2) =

_______

Answer: -4

Explanation:
Remember if the number being added is positive more number of units going to the right and if the number being added is negative more number of units to the left.
Since we are adding the negative number starting -2, we move 2 units to the left which gives the result -4.

Question 8.
-6 + (-8) =

_______

Answer: -14

Explanation:
Remember if the number being added is positive more number of units going to the right and if the number being added is negative more number of units to the left.
Since we are adding the negative number starting from -6 we have to move 8 units to left which shows the result -14.

Find each sum.

Question 9.
-5 + (-4) =
_______

Answer: -9

Explanation:
In adding two integers with the same signs you add both the integers and keep the standard sign.
Since -5 + (-4) has the same sign we add their absolute value and keep the same character.
-5 + (-4) = -(5 + 4) = -9

Adding Integers 7th Grade Question 10.
-1 + (-10) =
_______

Answer: -11

Explanation:
In adding two integers with the same signs you add both the integers and keep the standard sign.
Since -1 + (-10) has the same sign we add their absolute value and keep the same character.
-1 + (-10) = -(1 + 10)
= -11
So the answer is -11.

Question 11.
-9 + (-1) =
_______

Answer: -10

Explanation:
In adding two integers with the same signs you add both the integers and keep the common sign.
Since -9 + (-1) has the same sign we add their absolute value and keep the same sign.
-9 + -1 = -(9 + 1)
= -10
Thus the answer is -10.

Question 12.
-90 + (-20) =
_______

Answer: -110

Explanation:
In adding two integers with the same signs you add both the integers and keep the common sign.
Since -90 + (-20) has the same sign we add their absolute value and keep the same sign.
-90 + (-20) = -(90 + 20)
= -110
The answer is -110.

Question 13.
-52 + (-48) =
_______

Answer: -100

Explanation:
In adding two integers with the same signs you add both the integers and keep the common sign.
Since -52 + (-48) has the same sign we add their absolute value and keep the same sign.
-52 + (-48) = -(52 + 48)
= -100
The answer is -100.

Question 14.
5 + 198 =
_______

Answer: 203

Explanation:
In adding two integers with the same signs you add both the integers and keep the common sign.
Since 5 + 198 has the same sign we add their absolute value and keep the same sign.
5 + 198 = 203
The answer is 203.

Adding Integers Answers Question 15.
-4 + (-5) + (-6) =
_______

Answer: -15

Explanation:
In adding two integers with the same signs you add both the integers and keep the common sign.
Since -4 + (-5) + (-6) has the same sign we add their absolute value and keep the same sign.
-4 + (-5) + (-6) = -(4 + 5 + 6)
= -15
The answer is -15.

Question 16.
-50 + (-175) + (-345) =
_______

Answer: -570

Explanation:
In adding two integers with the same signs you add both the integers and keep the common sign.
Since -50 + (-175) + (-345) has the same sign we add their absolute value and keep the same sign.
-50 + (-175) + (-345)
= -(50 + 175 + 345)
= -570
The answer for -50 + (-175) + (-345) is -570.

Question 17.
How do you add integers with the same sign?
Type below:
______________

Answer:

First, you should their absolute values and keep the common sign. If both signs are positive, the answer will be positive. If both signs are negative, the answer will be negative.

Adding Integers with the Same Sign – Independent Practice – Page No. 11

Question 18.
Represent Real-World Problems Jane and Sarah both dive down from the surface of a pool. Jane first dives down 5 feet and then dives down 3 more feet. Sarah first dives down 3 feet, and then dives down 5 more feet.
a. Multiple Representations Use the number line to model the equation -5 + (-3) = -3 + (-5).

Type below:
______________

Answer: -8

Explanation:
Start at -3 and move 5 units down for one number line. Next, start at -5 and move down 3 units for another number line.
Both have a final answer of -8.
So, -5 + (-3) = -3 + (-5) = -8.

Question 18.
b. Does the order in which you add two integers with the same sign affect the sum? Explain.
_______

Answer: no

Explanation:

Based on the results of part a, the order doesn’t matter. Since the commutative properties of addition hold for the sum of two negative numbers.

Adding and Subtracting Integers Practice 7th Grade Question 19.
A golfer has the following scores for a 4-day tournament.

What was the golfer’s total score for the tournament?
_______

Answer: -11

Explanation:
The total score is the sum of each day’s score
= -3 + (-1) + (-5) + (-2)
= -(3 + 1 + 5 + 2)
= -11
Thus the total score for the 4-day tournament is -11.

Question 20.
A football team loses 3 yards on one play and 6 yards on another play. Write a sum of negative integers to represent this situation. Find the sum and explain how
It is related to the problem.
The sum = _______

Answer: -9

Explanation:
The negative sum of 3 yards and 6 yards is
-3 + (-6) = -(3 + 6)
= -9
Thus the negative sum is -9.

Question 21.
When the quarterback is sacked, the team loses yards. In one game, the quarterback was sacked four times. What was the total sack yardage?

_______

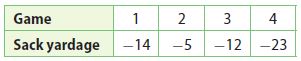
Answer: -54

Explanation:
The total sack yardage = -14 + (-5) + (-12) + (-23)
= -(14 + 5 + 12 + 23)
= -54
Therefore the total sack yardage is -54.

Question 22.
Multistep The temperature in Jonestown and Cooperville was the same at 1:00. By 2:00, the temperature in Jonestown dropped 10 degrees, and the temperature in Cooperville dropped 6 degrees. By 3:00, the temperature in Jonestown dropped 8 more degrees, and the temperature in Cooperville dropped 2 more degrees.
a. Write an equation that models the change to the temperature in Jonestown since 1:00.
Type below:
______________

Answer: J = T – 18

Explanation:
Let J be the final temperature and T be the initial temperature. Then the equation is J = T + (-10) + (-8)
J = T – 18

Question 22.
b. Write an equation that models the change to the temperature in Cooperville since 1:00.
Type below:
______________

Answer: C = T – 8

Explanation:
Let C be the final temperature and T be the initial temperature. Then the equation is C = T + (-6) + (-2)
C = T – 8

Question 22.
c. Where was it colder at 3:00, in Jonestown or Cooperville?
__________

Answer: Jonestown

Explanation:
Since they both started at the same temperature and Jonestown dropped a total of 18 degrees while Cooperville dropped a total of 8 degrees, Jonestown is colder.

Adding Integers with the Same Sign – Page No. 12

Question 23.
Represent Real-World Problems Julio is playing a trivia game. On his first turn, he lost 100 points. On his second turn, he lost 75 points. On his third turn, he lost 85 points. Write a sum of three negative integers that models the change to Julio’s score after his first three turns.
Type below:
______________

Answer: -260 points

Explanation:
The change in his total score is the sum of the losses = -100 + (-75) + (-85)
= -(100 + 75 + 85)
= -260 points
Thus Julio’s score after his first three turns is -260 points.

H.O.T. FOCUS ON HIGHER ORDER THINKING

Question 24.
Multistep On Monday, Jan made withdrawals of $25, $45, and $75 from her savings account. On the same day, her twin sister Julie made withdrawals of $35, $55, and $65 from her savings account.
a. Write a sum of negative integers to show Jan’s withdrawals on Monday. Find the total amount Jan withdrew.
Jan withdrew $ _______

Answer: 145

Explanation:
Each withdrawal is represented by a negative integer so find the sum of those negative integers = -25 + (-45) + (-75)
= -(25 + 45 + 75)
= -145
Thus Jan withdrew $145.

Question 24.
b. Write a sum of negative integers to show Julie’s withdrawals on Monday. Find the total amount Julie withdrew.
Julie withdrew $ _______

Answer: 155

Explanation:
Each withdrawal is represented by a negative integer so find the sum of those negative integers
= -35 + (-55) + (-65)
= – (35 + 55 + 65)
= -155
The total amount Julie withdrew is -$155.

Question 24.
c. Julie and Jan’s brother also withdrew money from his savings account on Monday. He made three withdrawals and withdrew $10 more than Julie did. What are three possible amounts he could have withdrawn?
Type below:
______________

Answer:

If he withdrew $10 more than Julie then he withdrew $165 in total. The possible amounts could then be $35, $55, $75.

Integers Addition and Subtraction Worksheet Grade 7 with Answers Question 25.
Communicate Mathematical Ideas Why might you want to use the Commutative Property to change the order of the integers in the following sum before adding?
-80 + (-173) + (-20)
Type below:
______________

Answer: You can add 80 and 20 easily to get 100 which is then easier to add 173. So changing the order makes the problem easier to do mentally.

Question 26.
Critique Reasoning The absolute value of the sum of two different integers with the same sign is 8. Pat says there are three pairs of integers that match this description. Do you agree? Explain.
__________

Answer: Disagree

Explanation:
Pat is saying that x + y = 8 is true for only three pairs of numbers with the same sign. This is not true though. The pairs could be 1, 7, 2 and 6, 3, 5, 4 and -4, -1 and -7, -2 and -6, -3 and -5 and -4, -4.

Adding Integers with Different Signs – Guided Practice – Page No. 16

Use a number line to find each sum.

Question 1.
9 + (-3) =

_______

Answer: 6

Explanation:
Remember if the number being added is positive more number of units going to the right and if the number being added is negative more number of units to the left.
Since we are adding a negative number starting from 9, move 3 units to the left. This results in 6.

Question 2.
-2 + 7 =

_______

Answer: 5

Explanation:
Remember if the number being added is positive more number of units going to the right and if the number being added is negative more number of units to the left.
Since we are adding a positive number starting from -2 we move 7 units to the right. This results in 5.

Adding Integers with Different Signs Answer Key Question 3.
-15 + 4 =

_______

Answer: -11

Explanation:
Remember if the number being added is positive more number of units going to the right and if the number being added is negative more number of units to the left.
Since we are adding a positive number starting from -15, we move 4 units to the right. This results in -11

Question 4.
1 + (-4) =

_______

Answer: -3

Explanation:
Remember if the number being added is positive more number of units going to the right and if the number being added is negative more number of units to the left.
Since we are adding the negative number starting from 1, we move 4 units to the left. This results in -3.

Circle the zero pairs in each model. Find the sum.

Question 5.
-4 + 5 =

_______

Answer: 1

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
Above is an illustration of which are the zero pairs and what remains. In this item 1 yellow counter remains which means the sum is 1.

Question 6.
-6 + 6 =

_______

Answer: 0

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
Above is an illustration of which are the zero pairs and what remains. In this item, there are no counters so the sum is 0.

Subtraction of Integers Grade 7 Question 7.
2 + (-5) =

_______

Answer: -3

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the standard sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger one and keep the sign of the number with the larger absolute value.
Above is an illustration of which are the zero pairs and what remains. In this item, 3 red counters are remaining so the sum is -3.

Question 8.
-3 + 7 =

_______

Answer: 4

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the standard sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger one and keep the sign of the number with the larger absolute value.
Above is an illustration of which are the zero pairs and what remains. In this item, 4 yellow counters remain so the sum is 4.

Find each sum.

Question 9.
-8 + 14 =
_______

Answer: 6

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the standard sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger one and keep the sign of the number with the larger absolute value.
Here we are the opposite number with the negative number.
-8 + 14 = 6
The larger number has a positive sign so the sum is 6.

Question 10.
7 + (-5) =
_______

Answer: 2

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
7 + (-5) = 7 – 5 = 2
The larger number has a positive sign so the sum is 2.

Question 11.
5 + (-21) =
_______

Answer: -16

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
5 + (-21) = 5 – 21 = -17
The larger number has a negative number so the sum is -17.

Question 12.
14 + (-14) =
_______

Answer: 0

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
14 + (-14) =14 – 14 = 0

Question 13.
0 + (-5) =

Answer: -5

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
0 + (-5) = 0 – 5 = -5
The larger is having the negative sign so the sum is -5.

Question 14.
32 + (-8) =
_______

Answer: 24

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the standard sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger one and keep the sign of the number with the larger absolute value.
32 + (-8) = 32 – 8 = 24
The larger number has a positive sign so the sum is 24.

Adding and Subtracting Integers 7th Grade Question 15.
Describe how to find the sums -4 + 2 and -4 + ( -2 ) on a number line.
Type below:
____________

Answer: -2

Explanation:
Start at -4 and move 2 units up for one number line. Next, start at -4 and move down 2 units for another number line.
-4 + 2 = -2
-4 – 2 = -6

Adding Integers with Different Signs – Independent Practice – Page No. 17

Find each sum.

Question 16.
-15 + 71 =
_______

Answer: 56

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
-15 + 71 = |71| – |-15|
= 71 – 15
= 56

Question 17.
-53 + 45 =
_______

Answer: -8

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
-53 + 45 = |-53| – |45|
53 – 45 = 8
The larger number is having the negative symbol so the answer is -8.

Question 18.
-79 + 79 =
_______

Answer: 0

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
79 + (-79) = |79| – |-79|
79 – 79 = 0

Question 19.
-25 + 50 =
_______

Answer: 25

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
-25 + 50 = |50| – |-25|
50 – 25 = 25

Adding and Subtracting Integers Worksheet Question 20.
18 + (-32) =
_______

Answer: -14

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
18 + (-32) = |-32| – |18|
32 – 18 = 14
The larger number is having a negative sign so the answer is -14.

Question 21.
5 + (-100) =
_______

Answer: -95

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
5 + (-100) = |-100| – |5|
100 – 5 = 95
The larger number is having a negative sign so the answer is -95.

Question 22.
-12 + 8 + 7 =
_______

Answer: 3

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
-12 + 8 + 7 = -12 + (8 + 7)
For the terms have different signs, we subtract the lesser absolute value from the greater absolute value and use the sign of the integer with the greater absolute value for the sum: 3
-12 + 15 = 3

Question 23.
-8 + (-2) + 3 =
_______

Answer: -7

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
-(8 + 2) + 3
For the terms have different signs, we subtract the lesser absolute value from the greater absolute value and use the sign of the integer with the greater absolute value for the sum: -7
-10 + 3 = -7

Question 24.
15 + (-15) + 200 =
_______

Answer: 200

Explanation:
We are given the expression:
15 + (-15) + 200 = 0 + 200
The sum of the opposite number is 0.
0 + 200 = 200

Question 25.
-500 + (-600) + 1200 =
_______

Answer: 100

Explanation:
We are given the expression:
-500 + (-600) + 1200 = -(500 + 600) + 1200
-1100 + 1200 = +100

Question 26.
A football team gained 9 yards on one play and then lost 22 yards on the next. Write a sum of integers to find the overall change in field position. Explain your answer.
Type below:
____________

Answer: -13

Explanation:
9 + (-22)
Since 9 yards are gained, the field position is changed by +9 and since 22 yards are lost the field position will be changed by -22, so we have:
(+9) + (-22) = -(22 – 9) = -13
We computer the overall change in field position: -13

Subtracting Integers Worksheet Answer Key Question 27.
A soccer team is having a car wash. The team spent $55 on supplies. They earned $275, including tips. The team’s profit is the amount the team made after paying for supplies. Write a sum of integers that represents the team’s profit.
Type below:
____________

Answer: 220

Explanation:
(-55) + (+275)
The money spent on supplies diminishes the profit, so they contribute to the profit with -55, while the earned money increases the profit, so they contribute to the profit with +275.
The sum of integers that represents the team’s profit is:
(-55) + (+275) = (275 -55) = 220

Question 28.
As shown in the illustration, Alexa had a negative balance in her checking account before depositing a $47.00 check. What is the new balance of Alexa’s checking account?

$ _______

Answer: 0

Explanation:
(-47) + 47 = 0
The new balance consists of the sum between the old balance and the amount she deposits: 0

Question 29.
The sum of two integers with different signs is 8. Give two possible integers that fit this description.
Type below:
____________

Answer: 10 and -2

Explanation:
10 and 2
10 – 2 = 8
Because the sum of the two numbers is positive and the two numbers have different signs, it means the absolute value of the positive number is 8 units greater than the absolute value of the negative number. First, we find two positive numbers which are different by 8, which will be the positive values of our numbers.
10 and -2
Our positive number will be the greater one while our negative number will be the smaller one (-2). So the desired numbers are:
10 + (-2) = 8
12 + (-4) = 8
15 + (-7) = 8

Question 30.
Multistep Bart and Sam played a game in which each player earned or lost points in each turn. A player’s total score after two turns is the sum of his points earned or lost. The player with the greater score after two turns wins. Bart earned 123 points and lost 180 points. Sam earned 185 points and lost 255 points. Which person won the game? Explain.
____________

Answer: Bart

Explanation:
123 + (-180) = -(180 – 123) = -57
The person who has the greatest number of points after 2 turns win.
We find the number of points Bart has, by adding the number of points from the two turns:
185 + (-255) = -(255 – 185) – 70
We find the number of points Sam has, by adding the number of points from the two turns:
The winner is Bart because -57 is greater than -70.

Adding Integers with Different Signs – Page No. 18

H.O.T. FOCUS ON HIGHER ORDER THINKING

Question 31.
Critical Thinking Explain how you could use a number line to show that -4 + 3 and 3 + (-4) have the same value. Which property of addition states that these sums are equivalent?
____________ Property of Addition

Answer: Commutative property of addition

Explanation:
In order to prove that -4 + 3 and 3 + (-4) have the same value we use the number line twice: -1 we start from -4 and we move 3 units in the positive direction to the right we get the sum -1.
We start from 3 and we move 4 units in the negative direction to the left where we find again -1.
The property of addition which states that the sum is the same no matter the order in which we add the terms is called commutative property.

Question 32.
Represent Real-World Problems Jim is standing beside a pool. He drops a weight from 4 feet above the surface of the water in the pool. The weight travels a total distance of 12 feet down before landing on the bottom of the pool. Explain how you can write a sum of integers to find the depth of the water.
Type below:
____________

Answer: 12 + (-4) = 8

Explanation:
Given that,
Jim is standing beside a pool.
He drops weight from 4 feet above the surface of the water in the pool.
The weight travels a total distance of 12 feet down before landing on the bottom of the pool.
12 + (-4) = 12 – 4 = 8
The depth of the water can be calculated by adding to the total distance of 12 feet the negative distance of -4 feet.

Question 33.
Communicate Mathematical Ideas Use counters to model two integers with different signs whose sum is positive. Explain how you know the sum is positive.
Type below:
____________

Answer: The result is positive because there are more positive counters than negative counters.

Explanation:
○○○○○○○
●●●
Let’s model the sum 7 + (-3) using counters we use 7 white counters for the positive numbers and 3 black counters for the negative numbers.
We pair each white counter with a black counter their sum is 0.
The result is +4 as we are left with 4 white counters.
The result is positive because there are more positive counters than negative counters.

Lesson 1 Understand Addition of Positive and Negative Integers Question 34.
Analyze Relationships You know that the sum of -5 and another integer is a positive integer. What can you conclude about the sign of the other integer? What can you conclude about the value of the other integer? Explain.
Type below:
____________

Answer:
We know that the sum is -5 and another integer is a positive integer. This means that the absolute value of the positive number is greater than the absolute value of -5.
The absolute value of -5 is 5, so the absolute value of the positive integer must be greater than 5. But because the number is positive, its absolute value is the number itself, so the positive number must be greater than 5.
-5 + 7 = 7 – 5 = 2

Subtracting Integers – Guided Practice – Page No. 22

Explain how to find each difference using counters.

Question 1.
5 – 8 =
_______

Answer: -3

Explanation:
5 – 8
We start with 5 black counters.
Since we have to subtract more black counters than we have (5 instead of 8), we add 3 zero pairs:
We subtract the 8 black counters: -3
We are left with 3 white counters, which means the result is -3.

Question 2.
-5 – (-3) =
_______

Answer: -2

Explanation:
-5 – (-3)
We have to find the difference:
We start with 5 black counters.
we subtract 3 black counters from the 5 black counters: -2
We are left with 2 black counters, which means the result is: -2

Use a number line to find each difference.

Question 3.
− 4 − 5 = − 4 + ( _______ ) = _______

Answer: -9

Explanation:
-4 – 5
We have to compute the difference:
-4 – 5 = -(4 + 5)
On a number line, we start from -4 and go to the left by 5 units:
-4 -5 = -9

Adding and Subtracting Integers Grade 7 Question 4.
1 − 4 = 1 + ( _______ ) = _______

Answer: -3

Explanation:
1 – 4
We have to compute the difference:
1 – 4 = 1 + (-4)
We replace the subtraction by addition with the opposite:
On a number line, we start from 1 and go to the left by 4 units:
1 – 4 = – 3
The result is -3.

Solve.

Question 5.
8 – 11 =
_______

Answer: -3

Explanation:
8 – 11
We have to perform the subtraction:
8 – 11 = 8 + (-11)
We replace subtraction by addition with the opposite number:
8 + (-11) = -3
We use the rule for adding integers: -3

Question 6.
-3 – (-5) =
_______

Answer: 2

Explanation:
-3 – (-5)
We have to perform the subtraction:
-3 – (-5) = -3 + 5
We replace subtraction by addition with the opposite number:
-3 + 5 = 2
We use the rule for adding integers: 2

Question 7.
15 – 21 =
_______

Answer: -6

Explanation:
15 – 21
We have to perform the subtraction:
15 – 21 = 15 + (21)
We replace subtraction by addition with the opposite number:
15 + (-21) = -6
We use the rule for adding integers: -6

Question 8.
-17 – 1 =
_______

Answer: -18

Explanation:
We have to perform the subtraction:
-17 – 1 = -17 + (-1)
We replace subtraction by addition with the opposite number:
-17 + (-1) = -18
We use the rule for adding integers: -18

Question 9.
0 – (-5) =
_______

Answer: 5

Explanation:
We have to perform the subtraction:
0 – (-5) = 0 + 5
We replace subtraction b addition with the opposite number:
0 + 5 = 5
We use the rule for adding integers: 5

Question 10.
1 – (-18) =
_______

Answer: 19

Explanation:
We have to perform the subtraction:
1 – (-18) = 1 + 18
We replace subtraction by addition with the opposite number:
1 + 18 = 19
We use the rule for adding integers: 19

Question 11.
15 – 1 =
_______

Answer: 14

Explanation:
We have to perform the subtraction:
15 – 1 = 14
We subtract the numbers directly as in this case it is simpler than to replace subtraction by addition with the opposite: 14

Question 12.
-3 – (-45) =
_______

Answer: 42

Explanation:
We have to perform the subtraction:
-3 – (-45) = -3 + 45
We replace subtraction by addition with the opposite number:
-3 + 45 = 42
We use the rule for adding integers: 42

Question 13.
19 – (-19) =
_______

Answer: 38

Explanation:
We have to perform the subtraction:
19 – (-19) = 19 + 19
We replace subtraction by addition with the opposite number:
19 + 19 = 38
We use the rule for adding integers: 38

Question 14.
-87 – (-87) =
_______

Answer: 0

Explanation:
We have to perform the subtraction:
-87 – (-87) = -87 + 87
We replace subtraction by addition with the opposite number:
-87 + 87 = 0
Ths um of opposite numbers is 0

Question 15.
How do you subtract an integer from another integer without using a number line or counters? Give an example.
Type below:
____________

Answer:
Integers with the same sign: Change to additions values then keep the common sign.
integers with different signs: Change to addition absolute value from larger value, the keep sign of larger absolute value.

Subtracting Integers – Independent Practice – Page No. 23

Question 16.
Theo had a balance of -$4 in his savings account. After making a deposit, he has $25 in his account. What is the overall change to his account?
$ _______

Answer: $29

Explanation:
Theo had a balance of -$4 in his savings account.
After making a deposit, he has $25 in his account.
25 – (-4)
The overall change to the account is the difference between the amount in the account after making the deposit and the amount before it, so we have to perform the subtraction.
25 – (-4) = 25 + 4
We change subtraction to addition with the opposite number:
25 + 4 = 29
We apply the rules for adding integers: $29

Adding and Subtracting Integers Worksheet Answer Key Question 17.
As shown, Suzi starts her hike at an elevation below sea level. When she reaches the end of the hike, she is still below sea level at -127 feet. What was the change in elevation from the beginning of Suzi’s hike to the end of the hike?

_______ feet

Answer: 98 feet

Explanation:
127 – (-225)
The change in the elevation from the beginning of Suzi’s hike to the end of the hike is the difference between the elevation at the end of the hike and the elevation at the beginning of it, so we have to perform the subtraction:
-127 – (-225) = -127 + 225
We change subtraction to addition with the opposite number:
-127 + 225 = 98
We apply the rules for adding integers: 98 feet

Question 18.
The record-high January temperature in Austin, Texas, is 90 °F. The record-low January temperature is -2 °F. Find the difference between the high and low temperatures.
_______ °F

Answer: 92°F

Explanation:
90 – (-2)
We have to find the difference between the high and low temperatures, so we have to perform the subtraction:
90 – (-2) = 90 + 2
We change subtraction to addition with the opposite number:
90 + 2 = 92 feet

Question 19.
Cheyenne is playing a board game. Her score was -275 at the start of her turn, and at the end of her turn, her score was -425. What was the change in Cheyenne’s score from the start of her turn to the end of her turn?
_______ °C

Answer: -150

Explanation:
-425 – (-275)
The change in Cheyenne’s score from the start of her turn to the end of her turn in the result of the subtraction:
-425 – (-275) = -425 + 275 = -150 points

Question 20.
A scientist conducts three experiments in which she records the temperature of some gases that are being heated. The table shows the initial temperature and the
final temperature for each gas.

a. Write a difference of integers to find the overall temperature change for each gas.
Gas A: __________ °C increase
Gas B: __________ °C increase
Gas C: __________ °C increase

Answer:
We determine the overall change of temperature for each gas by subtracting the initial temperature from the final temperature.
Gas A:
-8 – (-21) = -8 + 21 = 13
Gas B:
12 – (-12) = 12 + 12 = 24
Gas C:
-15 – (-19) = -15 + 19 = 4

Question 20.
What If? Suppose the scientist performs an experiment in which she cools the three gases. Will the changes in temperature be positive or negative for this experiment? Why?
__________

Answer: Negative

Explanation:
Cooling the gases means diminishing their temperature, thus their final temperature will be lower than the initial temperature, so the change in temperature will be negative.

Subtracting Integers – Page No. 24

Question 21.
Analyze Relationships For two months, Nell has fed her cat Diet Chow brand cat food. Then for the next two months, she feeds her cat Kitty Diet brand cat food. The table shows the cat’s change in weight over 4 months.

Which brand of cat food resulted in the greatest weight loss for Nell’s cat? Explain.
__________

Answer: Diet Chow

Explanation:
(-8) + (-18) = -26
We count the total change of weight resulting after using the diet chow for two months.
We count the total change of weight resulting after using the Kitty Diet for two months:
3 + (-19) = -16
This means that by using the Diet Chow the cat lost 26 oz, while using the Kitty Diet she lost 16 oz, thus the greatest loss of weight resulted in using the Diet Chow food.

FOCUS ON HIGHER ORDER THINKING

Question 22.
Represent Real-World Problems Write and solve a word problem that can be modeled by the difference -4 – 10.
Type below:
____________

Answer:
We have to write and solve a problem using the difference:
-4 – 10
For example:
Yesterday the temperature was -4 degrees. Today the temperature decreased by 10 degrees. What is the temperature today?
– 4 – 10 =- + (-10) = -14

Question 23.
Explain the Error When Tom found the difference -11 – (-4), he got -15. What might Tom have done wrong?
Type below:
____________

Answer:
We have to find the error in computing the difference:
-11 – (-4) = -15
In order to perform subtraction, Tom replaced it by addition, but he was wrong in adding -4 instead of adding its opposite 4.
The correct form is -11 – (-4) = -11 + 4 = -7

Question 24.
Draw Conclusions When you subtract one negative integer from another, will your answer be greater than or less than the integer you started with? Explain your reasoning and give an example.
____________ the integer

Answer: Greater

Explanation:
When we subtract one negative integer from another we will get an integer which is greater than the integer we started with because subtracting a negative integer from the initial number can be replaced by adding the opposite of that negative integer, which is a positive integer, thus the result will definitely be greater than the initial number.
-10 – (-3) = -10 + 3 = -7
-2 – (-7) = -2 + 7 = -5

Question 25.
Look for a Pattern Find the next three terms in the pattern 9, 4, −1, −6, −11, … . Then describe the pattern.
9, 4, -1, -6, -11, _______ , _______ , _______

Answer: -16, -21, -26

Explanation:
We are given the sequence of numbers:
9, 4 , -1, -6, -11,…
We find the next 3 terms:
-11 – 5 = -11 + (-5) = -16
-16 – 5 = 16 + (-5) = -21
-21 – 5 = -21 + (-5) = -26
Thus the next three terms are -16, -21, -26

Applying Addition and Subtraction of Integers – Guided Practice – Page No. 28

Write an expression. Then find the value of the expression.

Question 1.
Tomas works as an underwater photographer. He starts at a position that is 15 feet below sea level. He rises 9 feet, then descends 12 feet to take a photo of a coral reef. Write and evaluate an expression to find his position relative to sea level when he took the photo.
_______ feet below sea level

Answer: 18 feet

Explanation:
When he rises, we add the distance. When he descends, we subtract the distance.
The initial position is -15. We write an expression to find his position relative to sea level when he took the photo:
-15 + 9 – 12 = (-15) + 9 + (-12)
(-15) + (-12) + 9
-(15 + 12) + 9
-27 + 9 = -18
Thus he was 18 feet below sea level when he took the photo.

Applying Addition and Subtraction of Integers Question 2.
The temperature on a winter night was -23 °F. The temperature rose by 5 °F when the sun came up. When the sun set again, the temperature dropped by 7 °F. Write and evaluate an expression to find the temperature after the sunset.
_______ °F

Answer: -25

Explanation:
When the temperature rises, we add the temperature. When the temperature drops, we subtract the temperature. The initial temperature is -23.
We write an expression to find the temperature after the sunset:
-23 + 5 – 7 = -(23 + 7) + 5
-30 + 5 = -25
Thus the temperature is -25°F after the sunset.

Question 3.
Jose earned 50 points in a video game. He lost 40 points, earned 87 points, then lost 30 more points. Write and evaluate an expression to find his final score in the video game.
_______ points

Answer: 67 points

Explanation:
When he wins, we add points. When he loses, we subtract points.
The score is 50 points. We write the expression to find the final score:
50 – 40 + 87 – 30
50 + (-40) + 87 + (-30)
50 + 87 – (40 + 30)
137 – 70 = 67
Thus his final is 67 points.

Find the value of each expression.

Question 4.
-6 + 15 + 15 =
_______

Answer: 24

Explanation:
We have to find the value of the expression:
-6 + 15 + 15 = – 6 + 30 = 24
-6 + 15 + 15 = 24

Question 5.
9 – 4 – 17 =
_______

Answer: -12

Explanation:
We have to find the value of the expression:
9 – 4 – 17 = 9 – (4 + 17)
= 9 – 21 = -12

Question 6.
50 – 42 + 10 =
_______

Answer: 18

Explanation:
We have to find the value of the expression:
50 + (-42) + 10 = 60 – 42
We use the commutative property:
60 – 42 = 18

Question 7.
6 + 13 + 7 – 5 =
_______

Answer: 21

Explanation:
We have to find the value of the expression:
6 + 13 + 7 – 5 = 6 + 13 + 7 + (-5)
We use the associative property:
6 + 13 + 7 + (-5)
= (6 + 13 + 7) + (-5)
26 + (-5)
26 – 5 = 21

Applying Addition and Subtraction of Integers Question 8.
65 + 43 – 11 =
_______

Answer: 97

Explanation:
We have to find the value of the expression:
65 + 43 – 11 = 65 + 43 + (-11)
We use the associative property:
(65 + 43) – 11 = 97

Question 9.
-35 – 14 + 45 + 31 =
_______

Answer: 27

Explanation:
We have to find the value of the expression:
-35 – 14 + 45 + 31 = -(35 + 14) + 45 + 31
We use the associative property:
-(35 + 14) + 45 + 31
-49 + 76
= 27

Determine which expression has a greater value.

Question 10.
-12 + 6 – 4 or -34 – 3 + 39
___________

Answer:
We have to compare the expressions:
-12 + 6 – 4 or -34 – 3 + 39
We compute the first expression:
-12 + 6 – 4
-(12 + 4) + 6
-16 + 6 = -10
We compute the second expression:
-34 – 3 + 39
-(34 + 3) + 39
-37 + 39 = 2
2 > -10
Since 2 is greater than -10, the second expression is greater than the first expression.

Question 11.
21 – 3 + 8 or -14 + 31 – 6
___________

Answer:
We have to compare the expressions:
21 – 3 + 8 or -14 + 31 – 6
We compute the first expression:
21 – 3 + 8
21 + 8 – 3
21 + 5 = 26
We compute the second expression:
-14 + 31 – 6
31 – (14 + 6)
31 – 20 = 11
26 > 11
Since 26 is greater than 11, the first expression is greater than the second expression.

Question 12.
Explain how you can find the value of the expression -5 + 12 + 10 – 7.
Type below:
___________

Answer: 10

Explanation:
We have to find the value of the expression:
-5 + 12 + 10 – 7 = 12 + 10 – (5 + 7)
22 – 12 = 10

Applying Addition and Subtraction of Integers – Independent Practice – Page No. 29

Question 13.
Sports Cameron is playing 9 holes of golf. He needs to score a total of at most 15 over par on the last four holes to beat his best golf score. On the last four holes, he scores 5 over par, 1 under par, 6 over par, and 1 under par.
a. Write and find the value of an expression that gives Cameron’s score for 4 holes of golf.
Type below:
___________

Answer:
We write the expression that gives Cameron’s score for 4 holes:
5 – 1 + 6 – 1
5 + 6 – (1 + 1)
11 – 2 = 9

Question 13.
b. Is Cameron’s score on the last four holes over or under par?
Type below:
___________

Answer: The result shows that Cameron’s score is over par.

Question 13.
c. Did Cameron beat his best golf score?
_______

Answer:
Since his score of 9 is beaten his best score is 9 > 15.

Adding and Subtracting Integers Worksheet 7th Grade With Answers Question 14.
Herman is standing on a ladder that is partly in a hole. He starts out on a rung that is 6 feet underground, climbs up 14 feet, then climbs down 11 feet. What is Herman’s final position, relative to ground level?
_______ feet underground

Answer: 3 feet underground

Explanation:
Herman is standing on a ladder that is partly in a hole.
He starts out on a rung that is 6 feet underground, climbs up 14 feet, then climbs down 11 feet.
-6 + 14 -11
14 – (11 + 6)
14 – 17 = -3
Therefore the final position is 3 feet underground.

Question 15.
Explain the Error Jerome tries to find the value of the expression 3 – 6 + 5 by first applying the Commutative Property. He rewrites the expression as 3 – 5 + 6. Explain what is wrong with Jerome’s approach.
Type below:
___________

Answer: Jerome is wrong in using the Commutative Property at Subtraction which is not true: this property works for addition.
3 – 6 + 5 = 3 + (-6) + 5
3 + 5 – 6
= 8 – 6 = 2

Lesson 3 Add and Subtract Positive and Negative Integers Question 16.
Lee and Barry play a trivia game in which questions are worth different numbers of points. If a question is answered correctly, a player earns points. If a question is answered incorrectly, the player loses points. Lee currently has -350 points.

a. Before the game ends, Lee answers a 275-point question correctly, a 70-point question correctly, and a 50-point question incorrectly. Write and find the value of an expression to find Lee’s final score.
_______ points

Answer: -55 points

Explanation:
The initial score is -350 points. We write and find the value of an expression to find Lee’s final score:
-350 + 275 + 70 – 50
-(350 + 50) + 275 + 70
-400 + 345 = -55

Question 17.
b. Barry’s final score is 45. Which player had the greater final score?
___________

Answer: Since -55 < 45, it means Barry has a greater final score.

Question 17.
Multistep Rob collects data about how many customers enter and leave a store every hour. He records a positive number for customers entering the store each hour and a negative number for customers leaving the store each hour.

a. During which hour did more customers leave than arrive?
___________

Answer: 3:00 – 4:00

Explanation:
since in the last column the only positive value is in the last position, the hour in which more customers leave than arrive is 3:00 – 4:00

Question 17.
b. There were 75 customers in the store at 1:00. The store must be emptied of customers when it closes at 5:00. How many customers must leave the store between 4:00 and 5:00?
_______ customers

Answer: 87

Explanation:
75 + 30 – 12 + 14 – 8 + 18 – 30
75 + 30 + 14 + 18 – (12 + 8 + 30)
137 – 50 = 87
Since there are 87 customers in the store at 4:00 and the store must be emptied at 5:00, the number of clients who must leave is 87.

Applying Addition and Subtraction of Integers – Page No. 30

The table shows the changes in the values of two friends’ savings accounts since the previous month.

Question 18.
Carla had $100 in her account in May. How much money does she have in her account in August?
$ _______

Answer: $51

Explanation:
We are given the data:
100 – 18 + 22 – 53
100 + 22 -(18 + 53)
122 – 71 = 51
Thus Carla saved $51 in her account in August.

Question 19.
Leta had $45 in her account in May. How much money does she have in her account in August?
$ _______

Answer: $24

Explanation:
We are given the data:
45 – 17 – 22 + 18
45 + 18 -(17 + 22)
63 – 39 = 24
Thus Leta saved $24 in her account in August.

Question 20.
Analyze Relationships Whose account had the most significant decrease in value from May to August?
___________

Answer: Carla’s account

Explanation:
Carla had $100 in May and $51 in August, thus her account’s change is as:
51 – 100 = -49
Leta had $45 in May and $24 in August, thus her account change is:
24 – 45 = -21
Carla’s account had a decrease of $49, while Leta’s account decreased by $21, so the account with the greatest decrease is Carla’s.

FOCUS ON HIGHER ORDER THINKING

Question 21.
Represent Real-World Problems Write and solve a word problem that matches the diagram shown.

Type below:
___________

A diver leaves from a point situated 1 meter below the sea level. First, he dives 6 meters, then he rises 3 meters and stops. At which level under the sea level does he stop?
We start from the initial point -1, we add distance if he rises and we subtract distance when he dives. We determine the final level under the sea level where he stops:
-1 – 6 + 3
-(1 + 6) + 3
-7 + 3 = -4
-4 or 4 meters below the sea level.

Question 22.
Critical Thinking Mary has $10 in savings. She owes her parents $50. She does some chores and her parents pay her $12. She also gets $25 for her birthday from her grandmother. Does Mary have enough money to pay her parents what she owes them? If not, how much more money does she need? Explain.
_______

Answer:
The initial point is 10. We add money when she is paid for chores, gets presents. We determine,ine the amount of money she has after she gets money from chores and presents:
10 + 12 + 25 = 47
47 < 50
50 – 47 = 3
Thus she needs $3.

Question 23.
Draw Conclusions An expression involves subtracting two numbers from a positive number. Under what circumstances will the value of the expression be negative? Give an example.
Type below:
___________

Answer:
The sum of the two numbers to be subtracted from the positive number is a number, we will study this first. Since we subtract this number from the positive number and get a negative number, it means that the number is greater than the positive number, therefore mandatory positive. This means the two numbers cannot be both negative.
Example:
10 – (7 + 5) = 10 – 12 = -2
-2 < 0

Module Quiz – Ready to Go On – Page No. 31

Adding Integers with the Same Sign

Add

Question 1.
−8 + (−6) = _______

Answer: -14

Explanation:
In adding two integers with the same signs you add both the integers and keep the common sign.
−8 + (−6) = -(8 + 6) = -14

Adding and Subtracting Integers Question 2.
−4 + (−7) = _______

Answer: -11

Explanation:
In adding two integers with the same signs you add both the integers and keep the common sign.
−4 + (−7) = – 4 – 7
-(4 + 7) = -11
−4 + (−7) = -11

Question 3.
−9 + (−12) = _______

Answer: -21

Explanation:
In adding two integers with the same signs you add both the integers and keep the common sign.
−9 + (−12) = -9 – 12
-(9 + 12) = – 21
Thus −9 + (−12) = -21

Adding Integers with Different Signs

Add

Question 4.
5 + (−2) = _______

Answer: 3

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
5 + (−2) = 5 – 2 = 3
The larger number is having the positive sign thus the sum is 3

Question 5.
−8 + 4 = _______

Answer: -4

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
−8 + 4 = (-8) + 4 = -4
The larger number is having a negative sign thus the sum is -4.

Question 6.
15 + (−8) = _______

Answer: 7

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
15 + (−8) = 15 – 8 = 7
The larger number is having the positive sign thus the sum is 7.

Subtracting Integers

Subtract.

Question 7.
2 − 9 = _______

Answer: -7

Explanation:
2 – 9 = 2 + (-9)
|2| = 2
|-9| = 9
9 – 2 = 7
2 + (-9) = -7

Question 8.
−3 − (−4) = _______

Answer: 1

Explanation:
-3 – (-4) = – 3 + 4
4 – 3 = 1

Question 9.
11 − (−12) = _______

Answer: 23

Explanation:
11 − (−12) = 11 + 12 = 23

Applying Addition and Subtraction of Integers

Question 10.
A bus makes a stop at 2:30, letting off 15 people and letting on 9. The bus makes another stop ten minutes later to let off 4 more people. How many more or fewer people are on the bus after the second stop compared to the number of people on the bus before the 2:30 stop?
_______ people

Answer: 10

Explanation:
Assume that the total number of passengers on the bus before 2:30 was x
15 passengers got off and 9 got on.
number of passengers = x – 15 + 9
number of passengers = x -6
4 passengers got off the bus
number of passengers = (x-6) – 4
number of passengers = x – 10
The original number of passengers on the bus decreased by 10 after the second stop.

Adding and Subtracting Integers Word Problems with Answers Question 11.
Cate and Elena were playing a card game. The stack of cards in the middle had 24 cards in it to begin with. Cate added 8 cards to the stack. Elena then took 12 cards from the stack. Finally, Cate took 9 cards from the stack. How many cards were left in the stack?
_______ cards

Answer: 11 cards

Explanation:
When cards are put into the stack, we perform addition.
When cards are taken from the stack we perform subtraction.
24 + 8 – 12 – 9
32 – (12 + 9)
32 – 21 = 11
Thus in the end the stack has 11 cards.

ESSENTIAL QUESTION

Question 12.
Write and solve a word problem that can be modeled by the addition of two negative integers.
Type below:
_____________

Answer: -25

Explanation:
A football team played two games. During the first game, the team lost 15 points and during the second game, it lost another 10 points. What is the change in the team’s score after these two games?
(-15) + (-10) = -25

Module Quiz – MODULE 1 MIXED REVIEW – Page No. 32

Assessment Readiness

Selected Response

Question 1.
Which expression has the same value as -3 + (-5):
Options:
a. -3 – (-5)
b. -3 + 5
c. -5 + (-3)
d. -5 – (-3)

Answer: -5 + (-3)

Explanation:
a. -3 – (-5)
-3 + 5 = 2
b. -3 + 5
5 – 3 = 2
c. -5 + (-3)
– 5 – 3 = -8
d. -5 – (-3)
-5 + 3 = -2
Thus the correct answer is option C.

Question 2.
A diver’s elevation is -30 feet relative to sea level. She dives down 12 feet. What is her elevation after the dive?
Options:
a. 12 feet
b. 18 feet
c. -30 feet
d. -42 feet

Answer: -42 feet

Explanation:
A diver’s elevation is -30 feet relative to sea level. She dives down 12 feet.
-30 -12 = (-30) + (-12) = -42 feet
Thus the correct answer is option D.

Integer Math Problems Grade 7 Question 3.
Which number line models the expression -3 + 5?
Options:
a.
b.
c.
d.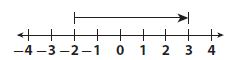

Answer:

Explanation:
-3 + 5
On the numeric line, his is modeled by starting at -3 and going right by 5 units. The number which models this is is:

Thus the correct answer is option B.

Question 4.
Which number can you add to 5 to get a sum of 0?
Options:
a. -10
b. -5
c. 0
d. 5

Answer: -5

Explanation:
The number we can add to 5 to get a sum of 0 is its opposite:
5 + (-5) = 0
The correct answer is option B.

Question 5.
The temperature in the morning was -3 °F. The temperature dropped 11 degrees by night. What was the temperature at night?
Options:
a. -14 °F
b. -8 °F
c. 8 °F
d. 14 °F

Answer: -14 °F

Explanation:
The temperature in the morning was -3 °F. The temperature dropped 11 degrees by night.
-3 + (-11) = -3 – 11 = -14°F
Therefore the correct answer is option A.

Question 6.
Which of the following expressions has the greatest value?
Options:
a. 3 – 7 + (-10)
b. 3 + 7 – (-10)
c. 3 – 7 – (-10)
d. 3 + 7 + (-10)

Answer: 3 + 7 – (-10)

Explanation:
a. 3 – 7 + (-10)
3 – 7 – 10 = 3 -(7 + 10) = 3 – 17 = -14
b. 3 + 7 – (-10)
3 + 7 + 10 = 20
c. 3 – 7 – (-10)
3 – 7 + 10 = 13 – 7 = 6
d. 3 + 7 + (-10)
10 – 10 = 0
Thus the correct answer is option B.

Mini-Task

Question 7.
At the end of one day, the value of a share of a certain stock was $12. Over the next three days, the change in the value of the share was -$1, then, -$1, and then $3.
a. Write an expression that describes the situation.
Type below:
____________

Answer:
We write an expression that describes the changes in the value of the share:
12 – 1 – 1 + 3

Question 7.
b. Evaluate the expression.
______

Answer: 13

Explanation:
12 – 1 – 1 + 3
12 + 3 – (1 + 1)
15 – 2 = 13

Question 7.
c. What does your answer to part b mean in the context of the problem?
Type below:
____________

Answer: After 3 days, the value of the share changed from $12 to $13.

MODULE 1

MIXED REVIEW

Assessment Readiness

Look at each expression. Does it have the same value as -6 – 4?

Select Yes or No for expressions A–C.

Question 8.
A. -6 + (-4)
______

Answer: Yes

Explanation:
-6 + (-4) = – 6 – 4
-6 + (-4) has the same value as – 6 – 4

Question 8.
B. -4 + (-6)
______

Answer: Yes

Explanation:
-4 + (-6) = -4 – 6
-4 + (-6) has the same value as – 6 – 4

Question 8.
C. 6 + (-4)
______

Answer: No

Explanation:
6 + (-4) = 6 – 4
6 – 4 ≠ – 6 – 4
So, 6 – 4 does not have the same value as – 6 – 4

Choose True or False for A–C.

Question 9.
A. x = 4 is the solution for x + 4 = 0.
i. True
ii. False

Answer: False

Explanation:
x + 4 = 0
x = 4
4 + 4 = 0
8 ≠ 0
So, the statement is false.

Question 9.
B. x = 24 is the solution for \(\frac{x}{3}\) = 8.
i. True
ii. False

Answer: True

Explanation:
\(\frac{x}{3}\) = 8
x = 24
24/3 = 8
8 = 8
Thus the statement is true.

Question 9.
C. x = 6 is the solution for 6x = 1
i. True
ii. False

Answer: False

Explanation:
6x = 1
x = 6
6(6) = 1
36 ≠ 1
Thus the statement is false.

Module 1 Review – Adding and Subtracting Integers – Page No. 103

EXERCISES

Question 1.
−10 + (−5) =
________

Answer: -15

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
-10 – 5 = -(10 + 5) = -15

Question 2.
9 + (−20) =
________

Answer: -11

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger one and keep the sign of the number with the larger absolute value.
9 + (-20) = 9 – 20 = -11

Integers Word Problems Grade 7 with Answers Pdf Question 3.
−13 + 32 =
________

Answer: 19

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger one and keep the sign of the number with the larger absolute value.
-13 + 32 = 32 + (-13)
32 – 13 = 19

Question 4.
−12 − 5 =
________

Answer: -17

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger one and keep the sign of the number with the larger absolute value.
-12 – 5 = -(12 + 5) = -17

Question 5.
25 − (−4) =
________

Answer: 29

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger one and keep the sign of the number with the larger absolute value.
25 − (−4) = 25 + 4 = 29

Question 6.
−3 − (−40) =
________

Answer: 37

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger one and keep the sign of the number with the larger absolute value.
-3 – (-40) = -3 + 40 = 37

Question 7.
Antoine has $13 in his checking account. He buys some school supplies and ends up with $5 in his account. What was the overall change in Antoine’s account?
$ ________

Answer: $8

Explanation:
The overall change in his account is given by the difference between the final amount of money and the initial amount of money
5 – 13 = 5 + (-13) = -8
The amount in his account is decreased by $8.

Conclusion:
Apply the concepts of math to real-time examples by learning the techniques using HMH Go Math Grade 7 Answer Key Chapter 1 Adding and Subtracting integers. The quick way of solving problems will help the students to save time. Stick to our Go Math Grade 7 Answer Key page to get brief explanations for all the chapters.

Get the detailed solutions for 7th Grade students in HMH Go Math Answer Key Chapter 6 Algebraic Expressions. We advise the students who are willing to score the highest marks in the exams to go through the Go Math Grade 7 Answer Key Chapter 6 Algebraic Expressions. Learn the concepts of mental calculation from our Go Math 7th Grade Solution Key Chapter 6 Algebraic Expressions.

Go Math Grade 7 Answer Key Chapter 6 Algebraic Expressions

Access the answers by downloading the Go Math Grade 7 Answer Key Chapter 6 Algebraic Expressions pdf. We have provided the step by step explanation topic wise. So, check out the topics before you start your preparation. After the preparation, you have a chance to test your math skills by solving the questions provided at the end of the chapter.

Chapter 6 Algebraic Expressions – Lesson:1

• Guided Practice – Page No. 176
• Independent Practice – Page No. 177
• Page No. 178

Chapter 6 Algebraic Expressions – Lesson:2

• Guided Practice – Page No. 182
• Independent Practice – Page No. 183
• Page No. 184

Chapter 6 Algebraic Expressions – Lesson:3

• Guided Practice – Page No. 188
• Independent Practice – Page No. 189
• Page No. 190

Chapter 6 Algebraic Expressions – Lesson:4

• Guided Practice – Page No. 194
• Page No. 195
• Page No. 196

Chapter 6 Algebraic Expressions

• 6.1 Algebraic Expressions – Page No. 197
• Selected Response – Page No. 198

Guided Practice – Page No. 176

Question 1.
The manager of a summer camp has 14 baseballs and 23 tennis balls. The manager buys some boxes of baseballs with 12 baseballs to a box and an equal number of boxes of tennis balls with 16 tennis balls to a box. Write an expression to represent the total number of balls.
______ + ______ n

Answer: 37 + 28n

Explanation:
Given that,
The manager of a summer camp has 14 baseballs and 23 tennis balls.
The manager buys some boxes of baseballs with 12 baseballs to a box and an equal number of boxes of tennis balls with 16 tennis balls to a box.
Let n be the number of boxes of each type
Baseballs: 14 + 12n
Tennis Balls: 23 + 16n
Now add the like terms
14 + 12n + 23 + 16n
(14 + 23) + (12 + 16)n
37 + 28n
Thus the expression for the total number of balls is 37 + 28n

Question 2.
Use the expression you found above to find the total number of baseballs and tennis balls if the manager bought 9 boxes of each type.

Answer: 289

Explanation:
The expression we found in the above question is 37 + 28n
n = 9 boxes
Substitute the value of n in the expression
37 + 28(9) = 37 + 252 = 289
Thus the total number of balls = 289

Use the Distributive Property to expand each expression.

Question 3.
0.5(12m – 22n)
______ m – ______ n

Answer: 6m – 11n

Explanation:
We use the Distributive Property to expand the expression.
0.5(12m – 22n) = 0.5(12m) – 0.5(22n)
= 16m – 11n
Thus the expansion of 0.5(12m – 22n) is 16m – 11n

Algebraic Expression Answer Key Question 4.
\(\frac{2}{3}\)(18x + 6z)
______ x + ______ z

Answer: 12x + 4z

Explanation:
We use the Distributive Property to expand the expression.
\(\frac{2}{3}\)(18x + 6z) = \(\frac{2}{3}\)(18x) + \(\frac{2}{3}\)(6z)
= \(\frac{36}{3}\) + \(\frac{12}{3}\)
= 12x + 4z
Thus the expansion of \(\frac{2}{3}\)(18x + 6z) is 12x + 4z

Factor each expression.

Question 5.
2x + 12
Type below:
_____________

Answer: 2(x + 6)

Explanation:
The common factor is 2. We factor the expression,
2x + 12 = 2(x + 6)

Question 6.
12x + 24
Type below:
_____________

Answer: 12(x + 2)

Explanation:
The common factor is 12. We factor the expression,
12x + 24 = 12(x + 2)

Question 7.
7x + 35
Type below:
_____________

Answer: 7(x + 5)

Explanation:
The common factor is 7. We factor the expression,
7x + 35 = 7(x + 5)

Essential Question Check-In

Question 8.
What is the relationship between multiplying and factoring?

Answer:
Factoring a number means writing it as a product – a list of numbers which when multiplied, give you the original number, thus factoring implies multiplication.
On the other hand, we can interpret the relationship between factoring and multiplication as one opposition because factoring an expression means dividing each term of the expression by the same number/factor.

Independent Practice – Page No. 177

Write and simplify an expression for each situation.

Question 9.
A company rents out 15 food booths and 20 game booths at the county fair. The fee for a food booth is $100 plus $5 per day. The fee for a game booth is $50 plus $7 per day. The fair lasts for d days, and all the booths are rented for the entire time. Write and simplify an expression for the amount in dollars that the company is paid.
______ + ______ d

Answer: 2500 + 215d

Explanation:
Given that,
A company rents out 15 food booths and 20 game booths at the county fair.
The fee for a food booth is $100 plus $5 per day.
The fee for a game booth is $50 plus $7 per day.
Let d be the number of days for which the booths are rented.
We have to write the expression for the amount of money for the food booths
15(100 + 5d)
We have to write the expression for the amount of money for the game booths
20(50 + 7d)
We have to write the expression for the amount of money for all the booths
15(100 + 5d) + 20(50 + 7d)
1500 + 75d + 1000 + 140d
Combine the like terms
2500 + 215d
Thus the expression for the amount in dollars that the company is paid is 2500 + 215d

Algebraic Expression Examples with Answers for Grade 7 Question 10.
A rug maker is using a pattern that is a rectangle with a length of 96 inches and a width of 60 inches. The rug maker wants to increase each dimension by a different amount. Let l and w be the increases in inches of the length and width. Write and simplify an expression for the perimeter of the new pattern.
______ + ______ l + ______ w

Answer:
A rug maker is using a pattern that is a rectangle with a length of 96 inches and a width of 60 inches. The rug maker wants to increase each dimension by a different amount.
The formula for the perimeter of a rectangle is 2 Length+ 2 Width
2 ×(96+l+60+w)
=2×(156+l+w)
=(312+2l+2w) inches

In 11 – 12, identify the two factors that were multiplied together to form the array of tiles. Then identify the product of the two factors.

Question 11.

______ x + ______

Answer: 3x + 6

Explanation:
The two factors are
Width = 3
Length = x + 2
The area is the product of the two numbers:
3(x + 2) = 3(x) + 3(2)
3x + 6

Question 12.

______ x – ______

Answer: 8x – 4

Explanation:
The two factors are
Width = 4
Length = 2x – 1
The area is the product of the two numbers:
4(2x – 1) = 4(2x) + 4(-1) = 8x – 4

Question 13.
Explain how the figure illustrates that 6(9) = 6(5) + 6(4).

Type below:
___________

Answer:
Note that the left part of the figure has 6 units from top to bottom and 5 units from left to right making it 6 × 5. On the other hand, the right part has also 6 units from top to bottom but 4 units from left to right making it 6 × 4. Adding the two expressions will give (6 × 5) + (6 × 4).

In 14–15, the perimeter of the figure is given. Find the length of the indicated side.

Question 14.

Type below:
_____________

Answer: 3x – 7

Explanation:
We know that the perimeter of a figure is the sum of all sides. Therefore, we can identify the length of the other side by representing it with a variable, s
side + side + side = perimeter
s + (x + 3) + (2x +4) = 6x
s + 3x + 7 = 6x
s = 6x – 3x – 7
Combine the like terms
s = 3x – 7

Question 15.

Type below:
_____________

Answer: 2x + 6

Explanation:
We know that the perimeter of a figure is the sum of all sides. Therefore, we can identify the length of the other side by representing it with a variable, s
2side + 2side = perimeter
2s + 2(3x – 3) = 10x + 6
2s + 6x – 6 = 10x + 6
2s = 10x + 6 -6x + 6
2s = 4x + 12
2s = 2(2x+ 6)
s = 2x + 6

Page No. 178

Question 16.
Persevere in Problem-Solving
The figures show the dimensions of a tennis court and a basketball court given in terms of the width x in feet of the tennis court.
a. Write an expression for the perimeter of each court.

Type below:
_____________

Answer:
Since the courts are rectangle, we can add all sides of the court using the given expressions:
Tennis:
x + x + (2x + 6) + (2x + 6)
= 2x + 4x + 12
= 6x + 12
Basketball:
(1/2 x + 32) + (1/2 x + 32) + (3x – 14) + (3x – 14)
x + 64 + 6x – 28
Now combine the like terms
7x + 36

Question 16.
b. Write an expression that describes how much greater the perimeter of the basketball court is than the perimeter of the tennis court.
Type below:
_____________

Answer: x + 24

Explanation:
Since the perimeter of the basketball court is larger, we subtract the perimeter of the tennis court from this.
Therefore the expression is (7x + 36) – (6x + 12)
= 7x + 36 – 6x – 12 = x + 24

Question 16.
c. Suppose the tennis court is 36 feet wide. Find all dimensions of the two courts.
Width of the tennis court: _________ feet
Length of the tennis court: _________ feet
Width of basketball court: _________ feet
Length of the basketball court: _________ feet

Answer:
To find all dimensions, we substitute 36 in x of the tennis court and solve for the length.
For the tennis court:
Width: x = 36 feet
Length: 2x + 6 = 2(36) + 6 = 72 + 6 = 78 feet
For the basketball court:
Width: 1/2 x + 32 = 1/21(36) + 32 = 18 + 32 = 50 feet
Length: 3x – 14 = 3(36) – 14 = 108 – 14 = 94 feet

Algebraic Expression 7th Grade Question 17.
Draw Conclusions
Use the figure to find the product (x + 3)(x + 2). (Hint: Find the area of each small square or rectangle, then add.)

Type below:
_____________

Answer: x² + 5x + 6

Explanation:
We can add the area of the smaller squares to find the area of the entire figure.
Note that there is one x.x = x²
There are 3(x.1) = 3x
There are 2(x.1) = 2x
There are 6(1.1) = 6
Adding these together we get x² + 3x + 2x + 6 = x² + 5x + 6

Question 18.
Communicate Mathematical Ideas
Desmond claims that the product shown at the right illustrates the Distributive Property. Do you agree? Explain why or why not.

________

Answer: Yes

Explanation:
The multiplication can be written:
58 × 23 = 58(20 + 3)
58(20) + 58(3)
1160 + 174
We notice that the products 174 and 1160 were obtained using the Distributive Property.

Question 19.
Justify Reasoning
Describe two different ways that you could find the product 8 × 997 using mental math. Find the product and explain why your methods work.
Type below:
_____________

Answer:
We are given the product
8 × 997
For a mental computation, we use the fact that 997 is close to 1000
8 × 997 = 8 . (1000 – 3)
8 × 1000 – 8 × 3
8000 – 24
7976
Other method:
8 × 997 = 8 . (900 + 90 + 7)
8(900) + 8(90) + 8(7)
7200 + 720 + 56
7976

Guided Practice – Page No. 182

The table shows the average temperature in Barrow, Alaska, for three months during one year.

Question 1.
How many degrees warmer is the average temperature in November than in January?
________ °F

Answer: 11.7°F

Explanation:
Let x represent the number of degrees the temperature in November is warmer than in January.
x + (-13.4) = -1.7
x – 13.4 + 13.4 = -1.7 + 3.4
x = 11.7
Thus the average temperature in November is 11.7°F warmer.

Question 2.
Suppose that during one period of extreme cold, the average daily temperature decreased 1 \(\frac{1}{2}\) °F each day. How many days did it take for the temperature to decrease by 9 °F?
________ days

Answer: 6 days

Explanation:
Let x be the number of days it took for the temperature to decrease by 9 °F
(-1 1/2)x = -9
-3/2x = -9
-3x = -18
x = 6
It took 6 days for the temperature to decrease by 9°F.

Use inverse operations to solve each equation.

Question 3.
−2x = 34
________

Answer: -17

Explanation:
We are given the equation:
−2x = 34
x = -17

Question 4.
y − 3.5 = −2.1
________

Answer: 1.4

Explanation:
We are given the equation:
y − 3.5 = −2.1
y = -2.1 + 3.5
y = 1.4

Question 5.
\(\frac{2}{3}\) z = −6
________

Answer: -9

Explanation:
We are given the equation:
\(\frac{2}{3}\) z = −6
z = -6 × \(\frac{3}{2}\)
z = -9

Essential Question Check-In

Question 6.
How does writing an equation help you solve a problem?
Type below:
_____________

Answer:
Writing an equation helps us model a problem. Once the equation is written, we can apply mathematical rules to determine the unknown in the equation.

Independent Practice – Page No. 183

The table shows the elevation in feet at the peaks of several mountains. Use the table for 7–9.

Question 7.
Mt. Everest is 8,707.37 feet higher than Mt. McKinley. What is the elevation of Mt. Everest?
________ feet

Answer: 29,087.87

Explanation:
Given that,
Mt. Everest is 8,707.37 feet higher than Mt. McKinley.
Add 8707.37 to the height of the Mt. McKinley to find the height of the Mt. Everest.
20,321.5 + 8,707.37 = 29,028.87
Thus the elevation of Mt. Everest is 29,087.87 feet

Question 8.
Liam descended from the summit of K2 to an elevation of 23,201.06 feet. How many feet did Liam descend? What was his change in elevation?
________ feet

Answer: 5050.25 feet

Explanation:
Given,
Liam descended from the summit of K2 to an elevation of 23,201.06 feet.
Subtract the height of the K2 mountain and his elevation after descending to find the number of feet he descended. Since he descended down the mountain the change in elevation is the negative of the number of feet he descended.
descent: 28,251.31 – 23,201.06 = 5050.25 feet
change in elevation: -5050.25 feet

Factoring Algebraic Expressions Worksheet 7th Grade Question 9.
K2 is 11,194.21 feet higher than Mt. Kenya. Write and solve an equation to find the elevation of Mt. Kenya.
________ feet

Answer: 17,057.1

Explanation:
Let h be the height of Mt. Kenya.
Write the equation using the given information that K2, with a height of 28,251.31 feet, is 11,194.21 feet higher than Mt. Kenya.
h + 11,194.21 = 28, 251.31
h = 17057.1 feet

Question 10.
A hot air balloon begins its descent at a rate of 22 \(\frac{1}{2}\) feet per minute. How long will it take for the balloon’s elevation to change by -315 feet?
________ minutes

Answer: 14 minutes

Explanation:
A hot air balloon begins its descent at a rate of 22 \(\frac{1}{2}\) feet per minute.
315/22 \(\frac{1}{2}\) = 315/\(\frac{45}{2}\)
= 315 × \(\frac{2}{45}\) = 14 minutes

Question 11.
During another part of its flight, the balloon in Exercise 10 had a change in elevation of -901 feet in 34 minutes. What was its rate of descent?
________ \(\frac{□}{□}\) feet per minute

Answer:

Divide the number of feet by the number of minutes
\(\frac{901}{34}\) = 26.5 feet per minute
(Or)
\(\frac{901}{10}\) = 90.1 feet per minute

The table shows the average temperatures in several states from January through March. Use the table for 12–14.

Question 12.
Write and solve an equation to find how much warmer Montana’s average 3-month temperature is than Minnesota’s.
________ °C

Answer: 1.8°C

Explanation:
Write an equation where t is the number of degrees warmer than Montana’s temperature is compared to Minnesota’s
-2.5 + t = -0.7
t = -0.7 + 2.5
t = 1.8°C

Question 13.
How much warmer is Florida’s average 3-month temperature than Montana’s?
________ °C

Answer: 18.8°C

Explanation:
Subtract Florida and Montana’s temperatures
18.1 – (-0.7) = 18.1 + 0.7 = 18.8°C

Question 14.
How would the average temperature in Texas have to change to match the average temperature in Florida?
________ °C

Answer: increase by 5.6°C

Explanation:
Subtract Florida and Texas’s temperatures
18.1 – 12.5 = 5.6 °C

Question 15.
A football team has a net yardage of −26 \(\frac{1}{3}\) yards on a series of plays. The team needs a net yardage of 10 yards to get a first down. How many yards do they have to get on their next play to get a first down?
________ \(\frac{□}{□}\) yards

Answer: 36 \(\frac{1}{3}\) yards

Explanation:
Subtract the final net yardage and the current net yardage to find how many more yards they need
10 – (−26 \(\frac{1}{3}\)) = 10 + 26 \(\frac{1}{3}\)
= 36 \(\frac{1}{3}\)
They have to get 36 \(\frac{1}{3}\) yards on their next play to get the first down.

Page No. 184

Question 16.
A diver begins at sea level and descends vertically at a rate of 2 \(\frac{1}{2}\) feet per second. How long does the diver take to reach -15.6 feet?
________ seconds

Answer: 6.24 seconds

Explanation:
Divide the number of feet the diver descends by the rate of descent.
time = distance/rate
\(\frac{-15.6}{-2.5}\)
= 6.24 seconds

Algebraic Equations Examples with Answers Grade 7 Question 17.
Analyze Relationships
In Exercise 16, what is the relationship between the rate at which the diver descends, the elevation he reaches, and the time it takes to reach that elevation?
Type below:
_____________

Answer: The elevation he reaches (y) is directly proportional to the time it takes to reach that elevation (x) and the rate of descent is (k) the constant of proportionality.

Question 18.
Check for Reasonableness
Jane withdrew money from her savings account in each of 5 months. The average amount she withdrew per month was $45.50. How much did she withdraw in all during the 5 months? Show that your answer is reasonable.
$ ________

Answer: $227.50

Explanation:
Multiply the amount she withdrew per month by the number of months.
45.50 × 5 = 227.50
Since 45.50 ≈ 50 and 50 × 5 = 250 which is close to 227.50, the answer is reasonable.

Question 19.
Justify Reasoning
Consider the two problems below. Which values in the problems are represented by negative numbers? Explain why.

(1) A diver below sea level ascends 25 feet to a reef at -35.5 feet. What was the elevation of the diver before she ascended to the reef?

(2) A plane descends 1.5 miles to an elevation of 3.75 miles. What was the elevation of the plane before its descent?
Type below:
_____________

Answer:
The elevation of -35.5 and the elevation after ascending are both represented by the negative numbers. The change in elevation is represented by a negative number since the plane is descending.

Question 20.
Analyze Relationships
How is solving -4x = -4.8 different from solving − \(\frac{1}{4}\) x = -4.8? How are the solutions related?
Type below:
_____________

Answer:
When you are solving -4x = -4.8, you are dividing both sides by -4 to solve for x.
When you are solving − \(\frac{1}{4}\) x = -4.8, you are multiplying both sides by -4 to solve for x.
The answer for the second equation is then 16 times the answer to the first problem since 4 × 4 = 16

Algebraic Expressions Simplify Question 21.
Communicate Mathematical Ideas
Flynn opened a savings account. In one 3-month period, he made deposits of $75.50 and $55.25. He makes withdrawals of $25.15 and $18.65. His balance at the end of the 3-month period is $210.85. Explain how you can find his initial deposit amount.
$ ________

Answer: $123.90

Explanation:
Let x be his initial deposit. Write the equation for his balance after making the additional deposits and withdrawals.
x + 75.50 + 55.25 – 25.15 – 18.65 = 210.58
x + 86.95 = 210.85
Simplify the left side of the equation
x = 123.90
Thus the initial deposit amount is $123.90

Guided Practice – Page No. 188

Draw algebra tiles to model the given two-step equation.

Question 1.
2x + 5 = 7
Type below:
_____________

Answer: 1

Explanation:

First, draw two positive rectangles on the left to represent 2x and five positive squares to represent 5. One the right side, draw 7 positive squares to represent 7.

Question 2.
−3 = 5 − 4x
Type below:
_____________

Answer: 2

Explanation:

Draw 3 negative squares on the left side to represent -3. On the right side, draw 5 positive squares to represent 5 and 4 negative rectangles to represent -4x.

Question 3.
A group of adults plus one child attend a movie at Cineplex 15. Tickets cost $9 for adults and $6 for children. The total cost for the movie is $78. Write an equation to find the number of adults in the group.
________ adults

Answer: 8 adults

Explanation:
Given,
A group of adults plus one child attend a movie at Cineplex 15.
Tickets cost $9 for adults and $6 for children.
The total cost for the movie is $78.
Write the equation for the total cost letting a be the number of adults.
9a + 6 = 78
9a = 72
a = 8
Therefore there are 8 adults in the group.

Question 4.
Break down the equation 2x + 10 = 16 to analyze each part.
Type below:
_____________

Answer:
Since x is the value we are trying to find, x is the solution. This means that 2x is the quantity we are looking for multiplied by 2. The 10 is added to 2x = 16 means the result is 16.

Question 5.
Write a corresponding real-world problem to represent 2x – 125 = 400.
Type below:
_____________

Answer:
A real-world problem could be: You are selling lemonade one summer. You paid a total of $125 for all the supplies you needed. If you charge customers $2 per cup of lemonade, how many cups of lemonade do you have to sell to make a profit of $400?

Essential Question Check-In

Question 6.
Describe the steps you would follow to write a two-step equation you can use to solve a real-world problem.
Type below:
_____________

Answer:
First, you must define what you are looking for with a variable. In the real-world problem, I wrote problem 5, the variable, x represents the number of cups sold. Next, decide how the remaining information is related to the variable. Since x is the number of cups sold and $2 is the price per cup, then the equation needs to have 2x.
Since profit = income – the cost of supplies, the cost of $125 needs to be subtracted from 2x and the equation needs to equal to the profit of $400. This would give an equation of 2x – 125 = 400.

Independent Practice – Page No. 189

Question 7.
Describe how to model -3x + 7 = 28 with algebra tiles.
Type below:
_____________

Answer:
On the left side, draw 3 negative rectangles to represent -3x and 7 positive squares to represent 7. On the right side, draw 28 positive squares to represent 28.

Question 8.
Val rented a bicycle while she was on vacation. She paid a flat rental fee of $55.00, plus $8.50 each day. The total cost was $123. Write an equation you can use to find the number of days she rented the bicycle.
________ days

Answer: 8 days

Explanation:
Let x be the number of days then the daily fees are 8.50x.
Since there is a flat fee of $55, the total fees are 8.50x + 55
8.50x + 55 = 123
8.50x = 123 – 55
8.50x = 68
x = 68/8.50
x = 8
Thus she rented the bicycle for 8 days.

Algebraic Expression Grade 7 Question 9.
A restaurant sells a coffee refill mug for $6.75. Each refill costs $1.25. Last month Keith spent $31.75 on a mug and refills. Write an equation you can use to find the number of refills that Keith bought.
________ refills

Answer: 20 refills

Explanation:
Given that,
A restaurant sells a coffee refill mug for $6.75.
Each refill costs $1.25. Last month Keith spent $31.75 on a mug and refills.
Let x represent the number of refills then the total for refills is 1.25x.
Since the cost of the mug was $6.75, the total cost is 6.75 + 1.25x
6.75 + 1.25x = 31.75
1.25x = 31.75 – 6.75
1.25x = 25
x = 25/1.25
x = 20
Thus the number of refills that Keith bought is 20 refills.

Question 10.
A gym holds one 60-minute exercise class on Saturdays and several 45-minute classes during the week. Last week all of the classes lasted a total of 285 minutes. Write an equation you can use to find the number of weekday classes.
________ classes

Answer: 5 classes

Explanation:
Given,
A gym holds one 60-minute exercise class on Saturdays and several 45-minute classes during the week.
Last week all of the classes lasted a total of 285 minutes.
Let x be the number of 45 minute classes then the total time of 45 minute classes if 45x the total time of all classes is then 60 + 45x = 285
45x = 285 – 60
45x = 225
x = 225/45
x = 5
Thus the number of weekday classes is 5.

Question 11.
Multiple Representations

There are 172 South American animals in the Springdale Zoo. That is 45 more than half the number of African animals in the zoo. Write an equation you could use to find n, the number of African animals in the zoo.
________ animals

Answer: 254 animals

Explanation:
There are 172 South American animals in the Springdale Zoo. That is 45 more than half the number of African animals in the zoo.
n/2 + 45 = 172
n/2 = 172 – 45
n/2 = 127
n = 127 × 2
n = 254 animals
Thus the number of African animals in the zoo is 254.

Question 12.
A school bought $548 in basketball equipment and uniforms costing $29.50 each. The total cost was $2,023. Write an equation you can use to find the number of uniforms the school purchased.
________ uniforms

Answer: 50 uniforms

Explanation:
The total cost is equal to the cost of the basketball equipment plus the cost of the uniforms.
Let x represent the number of uniforms. Since each uniform costs $29.50, then the cost of x uniforms is 29.50x dollars.
The cost of the basketball equipment is $548 so the total cost is 548 + 29.50x
It is given that the total cost is $2023 so setting this equal to the expression we obtained for the total cost gives the equation 548 + 29.50x = 2023
29.50x = 2023 – 548
29.50x = 1475
x = 1475/29.50
x = 50
Thus the number of uniforms the school purchased is 50.

Question 13.
Financial Literacy
Heather has $500 in her savings account. She withdraws $20 per week for gas. Write an equation Heather can use to see how many weeks it will take her to have a balance of $220.
________ weeks

Answer: 14 weeks

Explanation:
Given,
Heather has $500 in her savings account. She withdraws $20 per week for gas.
Let x be the number of weeks. Since she is withdrawing $20 each week, then after x weeks her account has changed by -20x dollars.
Her original balance was $500 so after x weeks, her ending balance is 500 – 20x dollars.
It is given that her ending balance is $220 so the equation is
500 – 20x = 220
-20x = 220 – 500
-20x = -280
x = 280/20
x = 14
It will take 14 weeks to have a balance of $220.

Algebra with Pizzazz Answer Key Page 190 Question 14.
Critique Reasoning
For 9x + 25 = 88, Deena wrote the situation “I bought some shirts at the store for $9 each and received a $25 discount. My total bill was $88. How many shirts did I buy?”
a. What mistake did Deena make?
Type below:
_____________

Answer: Her mistake was that a discount would decrease the amount she paid so her equation should have 25 subtracted, not added.

Question 14.
b. Rewrite the equation to match Deena’s situation.
Type below:
_____________

Answer: Changing the addition in 9x + 25 = 88 to subtraction gives 9x – 25 = 88

Question 14.
c. How could you rewrite the situation to make it fit the equation?
Type below:
_____________

Answer: Instead of a discount, the situation could be rewritten to have her buy another item, like pants or a sweater, that cost $25.

Page No. 190

Question 15.
Multistep
Sandy charges each family that she babysits a flat fee of $10 for the night and an extra $5 per child. Kimmi charges $25 per night, no matter how many children a family has.
a. Write a two-step equation that would compare what the two girls charge and find when their fees are the same.
Type below:
_____________

Answer: 10 + 5x = 25

Explanation:
Let x be the number of children.
Sandy charges each family that she babysits a flat fee of $10 for the night and an extra $5 per child. Kimmi charges $25 per night, no matter how many children a family has.
This means that she charges a total of 10 + 5x per night.
Kimmi only charges a flat fee of $25 per night,
Since you need to compare their charges, set these expressions equal to each other.
Sandy: 10 + 5x
Kimmi:  25
The equation is 10 + 5x = 25

Question 15.
b. How many children must a family have for Sandy and Kimmi to charge the same amount?
________ children

Answer: 3 children

Explanation:
Subtract 10 on both sides and then divide both sides by 5 to solve for x.
10 + 5x = 25
5x = 25 – 10
5x = 15
x = 3 children

Question 15.
c. The Sanderson family has five children. Which babysitter should they choose if they wish to save some money on babysitting, and why?
_____________

Answer: Kimmi, saves them $10

Explanation:
Substitute x = 5 in the above equation for Sandy.
10 + 5(5) = 10 + 25 = 35
This is $10 more than the $25 that Kimmi Charges so they should choose Kimmi because it will save them $10.

H.O.T.

Focus on Higher Order Thinking

Question 16.
Analyze Relationships
Each student wrote a two-step equation. Peter wrote the equation 4x – 2 = 10, and Andres wrote the equation 16x – 8 = 40. The teacher looked at their equations and asked them to compare them. Describe one way in which the equations are similar.
Type below:
_____________

Answer:
Each student wrote a two-step equation. Peter wrote the equation 4x – 2 = 10, and Andres wrote the equation 16x – 8 = 40.
4x – 2 = 10
4x = 10 + 2
4x = 12
x = 3
16x – 8 = 40
16x = 40 + 8
16x = 48
x = 48/16
x = 3
They are also similar because if you multiply both sides of 4x – 2 = 10 by 4, you get 16x – 8 = 40

Question 17.
What’s the Error?
Damon has 5 dimes and some nickels in his pocket, worth a total of $1.20. To find the number of nickels Damon has, a student wrote the equation 5n + 50 = 1.20. Find the error in the student’s equation.
Type below:
_____________

Answer:
The error is that he wrote the amount of money on the left side of the equation in cents but wrote the amount of money on the left side of the equation in dollars. He needs to write the equation as either 5n + 50 = 120. or 0.05n + 0.50 = 1.20

Question 18.
Represent Real-World Problems
Write a real-world problem you could answer by solving the equation -8x + 60 = 28.
Type below:
_____________

Answer:
A possible real-world problem could be: You have $60 to spend on clothes. You want to buy some T-shirts that cost $8 each. After you went shopping, you had $28 left. How many T-shirts did you buy?

Guided Practice – Page No. 194

The equation 2x + 1 = 9 is modeled below

Question 1.
To solve the equation with algebra tiles, first remove _____
Then divide each side into _____
Type below:
_____________

Answer:
The first step is to remove one positive square on each side. Then divide each side into 2 equal groups.

Question 2.
The solution is x = _____
x = ______

Answer: x = 4

Explanation:
The solution is x = 4 since removing one square on each side gives 2x = 8 and then dividing each side into two equal groups gives x = 4.

Solve each problem by writing and solving an equation.

Question 3.
A rectangular picture frame has a perimeter of 58 inches. The height of the frame is 18 inches. What is the width of the frame?
______ inches

Answer: 11 inches

Explanation:
A rectangular picture frame has a perimeter of 58 inches. The height of the frame is 18 inches.
The perimeter of a rectangle is P = 2w + 2h.
It is given that the perimeter of the rectangular frame is P = 58 inches and the height is h = 18 inches.
P = 2w + 2h
58 = 2w + 2(18)
2w = 58 – 36
2w = 22
w = 11 inches
Thus the width of the frame is 11 inches.

Question 4.
A school store has 1200 pencils in stock and sells an average of 24 pencils per day. The manager reorders when the number of pencils in stock is 500. In how many days will the manager have to reorder?
______ days

Answer: 30 days

Explanation:
A school store has 1200 pencils in stock and sells an average of 24 pencils per day.
The manager reorders when the number of pencils in stock is 500.
Let x be the number of days
1200 – 24x = 500
-24x = -700
x ≈ 30
Thus the manager has to reorder 30 days.

Essential Question Check-In

Question 5.
How can you decide which operations to use to solve a two-step equation?
Type below:
_____________

Answer:
You must use inverse operations when solving a two-step equation. You remove addition by subtracting the inverse operation of subtraction. You get rid of multiplication by using the inverse operation of division.

Page No. 195

Question 6.
9s + 3 = 57
______

Answer: 6

Explanation:
We are given the equation
9s + 3 = 57
9s = 57 – 3
9s = 54
s = 54/9
s = 6

Question 7.
4d + 6 = 42
______

Answer: 9

Explanation:
We are given the equation
4d + 6 = 42
4d = 42 – 6
4d = 36
d = 36/4
d = 9

Question 8.
−3y + 12 = −48
______

Answer: 20

Explanation:
We are given the equation
−3y + 12 = −48
-3y = -48 – 12
-3y = -60
3y = 60
y = 20

Question 9.
\(\frac{k}{2}\) + 9 = 30
______

Answer: 42

Explanation:
We are given the equation
\(\frac{k}{2}\) + 9 = 30
\(\frac{k}{2}\) = 30 – 9
k/2 = 21
k = 42

How to Simplify Algebraic Expressions Question 10.
\(\frac{g}{3}\) − 7 = 15
______

Answer: 66

Explanation:
We are given the equation
\(\frac{g}{3}\) − 7 = 15
\(\frac{g}{3}\) = 15 + 7
g/3 = 22
g = 22 × 3
g = 66

Question 11.
\(\frac{z}{5}\) + 3 = −35
______

Answer: -190

Explanation:
We are given the equation
\(\frac{z}{5}\) + 3 = −35
\(\frac{z}{5}\) = −35 – 3
z/5 = -38
z = -38 × 5
z = -190

Question 12.
−9h − 15 = 93
______

Answer: -12

Explanation:
We are given the equation
−9h − 15 = 93
-9h = 93 + 15
-9h = 108
-h = 108/9
h = -12

Question 13.
−3(n + 5) = 12
______

Answer: -9

Explanation:
We are given the equation
−3(n + 5) = 12
-3n – 15 = 12
-3n = 12 + 15
-3n = 27
-n = 27/3
n = -9

Question 14.
−17 + \(\frac{b}{8}\) = 13
______

Answer: 240

Explanation:
We are given the equation
−17 + \(\frac{b}{8}\) = 13
b/8 = 13 + 17
b/8 = 30
b = 30 × 8
b = 240

Question 15.
7(c − 12) = −21
______

Answer: 9

Explanation:
We are given the equation
7(c − 12) = −21
7c – 84 = -21
7c = -21 + 84
7c = 63
c = 63/7
c = 9

Question 16.
−3 + \(\frac{p}{7}\) = −5
______

Answer: -14

Explanation:
We are given the equation
−3 + \(\frac{p}{7}\) = −5
\(\frac{p}{7}\) = -5 + 3
\(\frac{p}{7}\) = -2
p = -2 × 7
p = -14

Question 17.
46 = −6t − 8
______

Answer: -9

Explanation:
We are given the equation
46 = −6t − 8
-6t – 8 = 46
-6t = 46 + 8
-6t = 54
-t = 54/6
t = -9

Question 18.
After making a deposit, Puja had $264 in her savings account. She noticed that if she added $26 to the amount originally in the account and doubled the sum, she would get the new amount. How much did she originally have in the account?
$ ______

Answer: $106

Explanation:
Let x be the original amount. Adding $26 to the original amount gives a sum of x + 26.
Doubling the sum then gives 2(x + 26) so the new amount is 2(x + 26) dollars.
It is given that the new amount is $264 so 2(x + 26) = 264
2(x + 26) = 264
x + 26 = 264/2
x + 26 = 132
x = 132 – 26
x = 106
Thus she originally has $106 in the account.

Question 19.
The current temperature in Smalltown is 20 °F. This is 6 degrees less than twice the temperature that it was six hours ago. What was the temperature in Smalltown six hours ago?
______ °F

Answer: 13°F

Explanation:
The current temperature in Smalltown is 20 °F. This is 6 degrees less than twice the temperature that it was six hours ago.
Let x be the temperature six hours ago
2x – 6 = 20
2x = 20 + 6
2x = 26
x = 13
Thus the temperature is 13°F in Smalltown six hours ago.

Question 20.
One reading at an Arctic research station showed that the temperature was -35 °C. What is this temperature in degrees Fahrenheit?
______ °F

Answer: -31°F

Explanation:
One reading at an Arctic research station showed that the temperature was -35 °C.
Substitute C = -35 into the formula for converting Celsius and Fahrenheit temperatures
C = 5/9 (F – 32)
-35 = \(\frac{5}{9}\)(F – 32)
-35 × \(\frac{9}{5}\) = F – 32
-7 × 9 = F – 32
-63 = F – 32
F = -63 + 32
F = -31°F
Thus the temperature in degrees Fahrenheit is -31°F

Question 21.
Artaud noticed that if he took the opposite of his age and adds 40, he gets the number 28. How old is Artaud?
______ years old

Answer: 12 years old

Explanation:
Artaud noticed that if he took the opposite of his age and adds 40, he gets the number 28.
Let x be his age
-x + 40 = 28
x = 40 – 28
x = 12
Thus Artaud is 12 years old.

Question 22.
Sven has 11 more than twice as many customers as when he started selling newspapers. He now has 73 customers. How many did he have when he started?
______ costumers

Answer: 31 customers

Explanation:
Let x be the number of customers he started with
11 + 2x = 73
2x = 73 – 11
2x = 62
x = 62/2
x = 31
Thus Sven had 31 customers when he started.

Question 23.
Paula bought a ski jacket on sale for $6 less than half its original price. She paid $88 for the jacket. What was the original price?
$ ______

Answer: $188

Explanation:
Given that,
Paula bought a ski jacket on sale for $6 less than half its original price. She paid $88 for the jacket.
Let x be the original price
1/2 x – 6 = 88
1/2 x = 88 + 6
1/2 x = 94
x = 94 × 2
x = 188
Thus the original price is $188.

Question 24.
The McIntosh family went apple picking. They picked a total of 115 apples. The family ate a total of 8 apples each day. After how many days did they have 19 apples left?
______ days

Answer: 12 days

Explanation:
The McIntosh family went apple picking. They picked a total of 115 apples. The family ate a total of 8 apples each day
Let x be the number of days.
115 – 8x = 19
115 – 19 = 8x
8x = 96
x = 96/8
x = 12
Thus the answer for the above question is 12 days.

Use a calculator to solve each equation.

Question 25.
−5.5x + 0.56 = −1.64
______

Answer: 0.4

Explanation:
We are given the equation
−5.5x + 0.56 = −1.64
Subtract 0.56 on both sides
-5.5x = -2.2
Divide both sides by -5.5
x = 0.4

Question 26.
−4.2x + 31.5 = −65.1
______

Answer: 23

Explanation:
We are given the equation
−4.2x + 31.5 = −65.1
Subtract 31.5 on both sides
-4.2x = -96.6
4.2x = 96.6
x = 96.6/4.2
x = 23

Question 27.
\(\frac{k}{5.2}\) + 81.9 = 47.2
______

Answer: -180.44

Explanation:
We are given the equation
\(\frac{k}{5.2}\) + 81.9 = 47.2
k/5.2 = 47.2 – 81.9
k/5.2 = -34.7
k = -180.44

Page No. 196

Question 28.
Write a two-step equation that involves multiplication and subtraction, includes a negative coefficient, and has a solution of x = 7.
Type below:
____________

Answer:
A possible two-step equation that involves multiplication and subtraction includes a negative coefficient, and has a solution of x = 7 is -2x – 7 = -21
-2x = -21 + 7
-2x = -14
2x = 14
x = 14/2
x = 7

Writing Algebraic Expressions Worksheet Question 29.
Write a two-step equation involving division and addition that has a solution of x = -25
Type below:
____________

Answer: \(\frac{x}{5}\) + 20 = 15

Explanation:
A possible two-step equation that involves division and addition and has a solution of x = -25 is \(\frac{x}{5}\) + 20 = 15
\(\frac{x}{5}\) = 15 – 20
\(\frac{x}{5}\) = -5
x = -25

Question 30.
Explain the Error
A student’s solution to the equation 3x + 2 = 15 is shown. Describe and correct the error that the student made.
3x + 2 = 15        Divide both sides by 3.
x + 2 = 5           Subtract 2 from both sides.
x = 3
\(\frac{□}{□}\)

Answer:
Her error was when she divided both sides by 3.
She didn’t divide the 2 by 3. She should have gotten x + \(\frac{2}{3}\) = 5 after dividing both sides by 3.
Her first step should have been subtracting both sides by 2 instead of dividing both sides by 3.
3x + 2 = 15
3x = 15 – 2
3x = 13
x = 13/2

Question 31.
Multiple Representations
Explain how you could use the work backward problem-solving strategy to solve the equation \(\frac{x}{4}\) − 6 = 2.
______

Answer: Working backward would mean talking the result of 2 and adding 6 to it to get 8. Then multiply this by 4 to get 32.

H.O.T.

Focus on Higher Order Thinking

Question 32.
Reason Abstractly
The formula F = 1.8C + 32 allows you to find the Fahrenheit (F) temperature for a given Celsius (C) temperature. Solve the equation for C to produce a formula for finding the Celsius temperature for a given Fahrenheit temperature.
Type below:
____________

Answer:
F = 1.8C + 32
F – 32 = 1.8C
1.8C = F – 32
C = (F – 32)/1.8

Question 33.
Reason Abstractly
The equation P = 2(l + w) can be used to find the perimeter P of a rectangle with length l and width w. Solve the equation for w to produce a formula for finding the width of a rectangle given its perimeter and length.
Type below:
____________

Answer:
P = 2(l + w)
P/2 = l + w
P/2 – l = w
w = P/2 – l

Question 34.
Reason Abstractly
Solve the equation ax + b = c for x.
Type below:
____________

Answer:
Subtract both sides by b
ax = c – b
x = (c – b)/a

6.1 Algebraic Expressions – Page No. 197

Question 1.
The Science Club went on a two-day field trip. The first day the members paid $60 for transportation plus $15 per ticket to the planetarium. The second day they paid $95 for transportation plus $12 per ticket to the geology museum. Write an expression to represent the total cost for two days for the n members of the club.
Type below:
____________

Answer: 155 + 27n

Explanation:
Let n be the number of members. Then n also represents the number of tickets.
For the first day, tickets are $15 each so for n members, the ticket cost is 15n dollars. The members must also pay $60 for transportation so the total cost for the first day is 60 + 15n dollars.
For the second day, tickets are $12 each so for n members, the ticket cost is 12n dollars. The members must also pay $95 for transportation so the total cost for the first day is 95 + 12n dollars.
The total cost for the two days is then (60 + 15n) + (95 + 12n).
Combine the like terms.
27n + 155

6.2 One-Step Equations with Rational Coefficients

Solve.

Question 2.
h + 9.7 = −9.7
______

Answer: h = -19.4

Explanation:
We are given the equation
h + 9.7 = −9.7
h = -9.7 – 9.7
h = -19.4

Question 3.
\(-\frac{3}{4}+p=\frac{1}{2}\)
\(\frac{□}{□}\)

Answer: p = 1 \(\frac{1}{4}\)

Explanation:
We are given the equation
\(-\frac{3}{4}+p=\frac{1}{2}\)
-3/4 + p = 1/2
p = 1/2 + 3/4
p = 1 \(\frac{1}{4}\)

Question 4.
−15 = −0.2k
______

Answer: k = 75

Explanation:
We are given the equation
−15 = −0.2k
0.2k = 15
k = 15/0.2
k = 150/2
k = 75

Question 5.
\(\frac{y}{-3}=\frac{1}{6}\)
\(\frac{□}{□}\)

Answer: y = – \(\frac{1}{2}\)

Explanation:
We are given the equation
\(\frac{y}{-3}=\frac{1}{6}\)
y = -3/6
y = -1/2

Question 6.
−\(\frac{2}{3}\) m = −12
______

Answer: m = 18

Explanation:
We are given the equation
−\(\frac{2}{3}\) m = −12
\(\frac{2}{3}\) m = 12
m = 12 × 3/2
m = 6 × 3
m = 18

Question 7.
2.4 = −\(\frac{t}{4.5}\)
______

Answer: t = -10.8

Explanation:
We are given the equation
2.4 = −\(\frac{t}{4.5}\)
-t = 2.4 × 4.5
t = -10.8

6.3 Writing Two-Step Equations

Question 8.
Jerry started doing sit-ups every day. The first day he did 15 sit-ups. Every day after that he did 2 more sit-ups than he had done the previous day. Today Jerry did 33 sit-ups. Write an equation that could be solved to find the number of days Jerry has been doing sit-ups, not counting the first day.
______ days

Answer: 2x + 15 = 33

Explanation:
Let x be the number of days then the number of additional sit-ups is 2x since he does 2 more sit-ups for each day, not counting the first day.
Since he started doing 15 sit-ups on the first day, the total number of sit-ups after x would be 2x +15
2x + 15 = 33

6.4 Solving Two-Step Equations

Solve.

Question 9.
5n + 8 = 43
______

Answer: n = 7

Explanation:
We are given the equation
5n + 8 = 43
5n = 43 – 8
5n = 35
n = 35/5
n = 7

Question 10.
\(\frac{y}{6}\) − 7 = 4
______

Answer: y = 66

Explanation:
We are given the equation
\(\frac{y}{6}\) − 7 = 4
\(\frac{y}{6}\) = 4 + 7
\(\frac{y}{6}\) = 11
y = 11 × 6
y = 66

Question 11.
8w − 15 = 57
______

Answer: w = 9

Explanation:
We are given the equation
8w − 15 = 57
8w = 57 + 15
8w = 72
w = 72/8
w = 9

Question 12.
\(\frac{g}{3}\) + 11 = 25
______

Answer: g = 42

Explanation:
We are given the equation
\(\frac{g}{3}\) + 11 = 25
\(\frac{g}{3}\) = 25 – 11
\(\frac{g}{3}\) = 14
g = 14 × 3
g = 42

Question 13.
\(\frac{f}{5}\) − 22 = −25
______

Answer: f = -15

Explanation:
We are given the equation
\(\frac{f}{5}\) − 22 = −25
\(\frac{f}{5}\) = -25 + 22
\(\frac{f}{5}\) = -3
f = -3 × 5
f = -15

Question 14.
−4p + 19 = 11
______

Answer: p = 2

Explanation:
We are given the equation
−4p + 19 = 11
-4p = 11 – 19
-4p = -8
p = 2

Essential Question

Question 15.
How can you use two-step equations to represent and solve real-world problems?
Type below:
___________

Answer:
You can use two-step equations to represent and solve real-world problems by translating the words into an algebraic equation, solving the equation, and then interpreting the solution to the equation.

Selected Response – Page No. 198

Question 1.
A taxi cab costs $1.50 for the first mile and $0.75 for each additional mile. Which equation could be solved to find how many miles you can travel in a taxi for $10, given that x is the number of additional miles?
Options:
a. 1.5x + 0.75 = 10
b. 0.75x + 1.5 = 10
c. 1.5x − 0.75 = 10
d. 0.75x − 1.5 = 10

Answer: 0.75x + 1.5 = 10

Explanation:
Let x be the number of additional miles then the charge for the additional miles is 0.75x the total cost is then 1.50 + 0.75x = 10
Thus the correct answer is option B.

Question 2.
Which is the solution of \(\frac{t}{2.5}\) = −5.2?
Options:
a. -13
b. -2.08
c. 2.08
d. 13

Answer: -13

Explanation:
t/2.5 = -5.2
t = -5.2 × 2.5
t = -13
Thus the correct answer is option A.

Question 3.
Which expression is equivalent to 5x − 30?
Options:
a. 5(x − 30)
b. 5(x − 6)
c. 5x(x − 6)
d. x(5 − 30)

Answer: 5(x − 6)

Explanation:
Factor out 5 from each term.
5x – 30 = 5(x – 6)
Thus the correct answer is option B.

Question 4.
In a science experiment, the temperature of a substance is changed from 42 °F to -54 °F at an average rate of -12 degrees per hour. Over how many hours does the change take place?
Options:
a. -8 hours
b. 18 hour
c. 1 hour
d. 8 hours

Answer: 8 hours

Explanation:
In a science experiment, the temperature of a substance is changed from 42 °F to -54 °F at an average rate of -12 degrees per hour.
Let x be the number of hours.
42 – 12x = -54
-12x = -54 – 42
-12x = -96
12x = 96
x = 96/12
x = 8 hours
Thus the correct answer is option D.

Question 5.
Which statement best represents the distance on a number line between -14 and -5?
Options:
a. −14 − (−5)
b. −14 + (−5)
c. −5 − (−14)
d. −5 + (−14)

Answer: −5 − (−14)

Explanation:
Distance is the difference between the biggest number and the smallest number so the distance between -5 and -14 is -5 – (-14) since -5 bigger than -14.
Thus the correct answer is option C.

Question 6.
Which cereal costs the most per ounce?
Options:
a. $4.92 for 12 ounces
b. $4.25 for 10 ounces
c. $5.04 for 14 ounces
d. $3.92 for 8 ounces

Answer: $3.92 for 8 ounces

Explanation:
Find the unit rates for each answer choice by dividing the cost by the number of ounces and rounding to two decimal places if necessary.
a. $4.92 for 12 ounces
4.92/12 = $0.41 per ounce
b. $4.25 for 10 ounces
4.25/10 ≈ 0.43 per ounce
c. $5.04 for 14 ounces
5.04/14 = 0.36 per ounce
d. $3.92 for 8 ounces
3.92/8 = 0.49 per ounce
Thus the correct answer is option D.

Mini-Task

Question 7.
Casey bought 9 tickets to a concert. The total charge was $104, including a $5 service charge.
a. Write an equation you can solve to find c, the cost of one ticket.
Type below:
_____________

Answer: 9c + 5 = 104

Explanation:
Let c be the cost of each ticket, the total cost of 9 tickets before the service charge is 9c adding the service charge gives a total charge of 9c + 5

Question 7.
b. Explain how you could estimate the solution of your equation.
Type below:
_____________

Answer:
104 is about 105. Subtracting 5 from this gives 100. 9 is about 10 and 100 divided by 10 is 10 so the ticket price is around $10.

Question 7.
c. Solve the equation. How much did each ticket cost?
$ ______

Answer:
9c = 99
c = 99/9
c = 11

Conclusion:

The concept of algebra is helpful for the students in the real life. So, it is very important for the 7th standard students to learn the tricks and use them the real-time. Bookmark our Go Math Answer Key to get a brief explanation for all the chapters. All the Best!!!!