Go Math Grade 6 Answer Key Chapter 6 Convert Units of Length
Learn the multiple ways to solve a problem using Go Math Grade 6 Answer Key Chapter 6 Convert Units of Length. Top math experts are worked to provide the best and simple solutions for students. The students who want to prepare math easily, they can use the Go Math Grade 6 Chapter 6 Convert Units of Length Solution Key. Learn Online maths using HMH Go Math Grade 6 Answer Key.
Go Math Grade 6 Chapter 6 Convert Units of Length Answer Key
You can find the ultimate guide to learn the Convert Units of Lengths i.e, HMH Go Math Grade 6 Answer Key. Start enjoying maths with the help of Go Math Grade 6 Convert Units of Length Answer Key. Go Math Grade 6 Chapter 6 Convert Units of Length Solution Key is free. So, quickly begin your practice by getting your Grade 6 Go Math Answer Key PDF Now.
Lesson 1: Convert Units of Length
- Convert Units of Length – Page No. 317
- Convert Units of Length – Page No. 318
- Convert Units of Length – Page No. 319
- Convert Units of Length Lesson Check – Page No. 320
Lesson 2: Convert Units of Capacity
- Convert Units of Capacity – Page No. 323
- Convert Units of Capacity – Page No. 324
- Convert Units of Capacity – Page No. 325
- Convert Units of Capacity Lesson Check – Page No. 326
Lesson 3: Convert Units of Weight and Mass
- Convert Units of Weight and Mass – Page No. 329
- Convert Units of Weight and Mass – Page No. 330
- Convert Units of Weight and Mass – Page No. 331
- Convert Units of Weight and Mass Lesson Check – Page No. 332
Mid-Chapter Checkpoint
Lesson 4: Transform Units
- Transform Units – Page No. 337
- Transform Units – Page No. 338
- Transform Units – Page No. 339
- Transform Units Lesson Check – Page No. 340
Lesson 5: Problem Solving • Distance, Rate, and Time Formulas
- Distance, Rate, and Time Formulas – Page No. 343
- Distance, Rate, and Time Formulas – Page No. 344
- Distance, Rate, and Time Formulas – Page No. 345
- Distance, Rate, and Time Formulas Lesson Check – Page No. 346
Chapter 6 Review/Test
- Review/Test – Page No. 347
- Review/Test – Page No. 348
- Review/Test – Page No. 349
- Review/Test – Page No. 350
- Review/Test – Page No. 351
- Review/Test – Page No. 352
Share and Show – Page No. 317
Convert to the given unit.
Question 1.
3 miles = ? yards
_______ yd
Answer:
5280 yd
Explanation:
3 miles = ? yards
1 yard = 3 feet
1 mile = 5280 feet
So, 3 miles = 3 x 5280 feet
= 15,840 feet
3 feet = 1 yard
Then, 15,840 feet = 15,840 ÷ 3
= 5280 yards
So, 3 miles = 5280 yards
Question 2.
43 dm = ? hm
_______ hm
Answer:
0.043 hm
Explanation:
43 dm= ?hm
10 decimeters = 1 meter
1 hectometer = 100 meters
1 meter = 10 decimeter
100 meters = 10×100 decimeters = 1000 decimeters
So 1 hectometer = 1000 decimeters
Then, 43 decimeters = 43/1000 = 0.043 hectometers
So, 43 dm = 0.043 hm
Question 3.
9 yd = ? in.
_______ inches
Answer:
324 inches
Explanation:
9 yd= ? in.
1 yard = 36 inches
So 9 yards = 9×36 = 324 inches
9 yards = 324 inches
Question 4.
72 ft = 24 yd
_______ yd
Answer:
24 yd
Explanation:
72 ft = 24 yd
1 yard = 3 feet
So, 1 feet = 1/3 yard
Then, 72 feet = 72/3 yard
So, 72 feet = 24 yards
Question 5.
7,500 mm = ? dm
_______ dm
Answer:
75 dm
Explanation:
7,500 mm = ?dm
1000 millimeters = 1 meter
10 decimeters = 1 meter
So, 1000 millimeters = 10 decimeters
Then 1 millimeter = 10/1000 decimeter = 1/100 decimeters
So 7500 millimeters = 7500/100 decimeters
Then 7500 mm = 75 dm
On Your Own
Question 6.
Rohan used 9 yards of ribbon to wrap gifts. How many inches of ribbon did he use?
_______ inches
Answer:
324 inches
Explanation:
As per the given data,
Rohan used 9 yards of ribbon to wrap gifts
1 yard = 36 inches
So, 9 yards = 9×36 = 324 inches
So, Rohan used 324 inches of ribbon to wrap gifts
Lesson 6 Classwork 6.1 Question 7.
One species of frog can grow to a maximum length of 12.4 millimeters. What is the maximum length of this frog species in centimeters?
_______ cm
Answer:
1.24 cm
Explanation:
One species of frog can grow to a maximum length of 12.4 millimeters.
From the given information
One species of frog can grow to a maximum length of 12.4 millimeters
1000 millimeters = 1 meter
100 centimeters = 1 meter
So, 1000 millimeters = 100 centimeters
1 millimeter = 100/1000 centimeters = 1/10 centimeters
So, 12.4 millimeters = 12.4/10 centimeters = 1.24 centimeters
12.4 millimeters = 1.24 centimeters
Question 8.
The height of the Empire State Building measured to the top of the lightning rod is approximately 443.1 meters. What is this height in hectometers?
_______ hectometers
Answer:
4.431 hectometers
Explanation:
The height of the Empire State Building measured to the top of the lightning rod is approximately 443.1 meters.
443.1 meters in hectometers
1 hectometer = 100 meters
Then, 1 meter = 1/100 hectometers
So, 443.1 meters = 443.1/100 hectometers
443.1 meters = 4.431 hectometers
Question 9.
A snail moves at a speed of 2.5 feet per minute. How many yards will the snail have moved in half of an hour?
_______ yards
Answer:
25 yards
Explanation:
From the given information
A snail moves at a speed of 2.5 feet per minute
1 hour = 60 minutes
1 minute = 2.5 feet speed
60 minutes = 60×2.5 feet = 150 feet
1 yard = 3 feet
So 1 feet = 1/3 yards
Then, 150 feet = 150/3 yards = 50 yards per hour
For half of an hour, a snail moves 25 yards
Practice: Copy and Solve Compare. Write <, >, or =.
Question 10.
32 feet _______ 11 yards
Answer:
32 feet < 11 yards
Explanation:
32 feet _______ 11 yards
1 yard = 3 feet
So, 11 yards = 11×3 = 33 feet
So, 32 feet < 11 yards
Question 11.
537 cm _______ 5.37 m
Answer:
537 cm = 5.37 m
Explanation:
537 cm _______ 5.37 m
100 centimeters = 1 meter
1 centimeter = 0.01 meter
So, 537 centimeters = 537×0.01 meters
That is 537 centimeters = 5.37 meters
Question 12.
75 inches _______ 6 feet
Answer:
75 inches > 6 feet
Explanation:
75 inches _______ 6 feet
1 foot = 12 inches
6 feet = 6×12 = 72 inches
So, 75 inches > 6 feet
Problem Solving + Applications – Page No. 318
What’s the Error?
Question 13.
The Redwood National Park is home to some of the largest trees in the world. Hyperion is the tallest tree in the park, with a height of approximately 379 feet. Tom wants to find the height of the tree in yards.
Tom converted the height this way :
3 feet = 1 yard
conversion factor: \(\frac{3 \mathrm{ft}}{1 \mathrm{yd}}\)
\(\frac{379 \mathrm{ft}}{1} \times \frac{3 \mathrm{ft}}{1 \mathrm{yd}}\) = 1,137 yd
Find and describe Tom’s error.
Show how to correctly convert from 379 feet to yards.
Explain how you knew Tom’s answer was incorrect.
Type below:
____________
Answer:
conversion factor: 3ft1yd
379ft1 × 3ft1yd = 1,137 yd
We need to divide the 379 feet with 3 to get the height of the Hyperion tree, but tom multiplies the 379 with 3 and that is the error part
1 yard = 3 feet
1 feet = 1/3 yards
So, 379 feet = 379/3 yards = 126.3 yards
So, the height of the Hyperion tree is 126.3 yards
Question 14.
Choose <, >, or =.
14a. 12 yards Ο 432 inches
14b. 321 cm Ο 32.1 m
12 yards _______ 432 inches
321 cm _______ 32.1 m
Answer:
14a. 12 yards Ο 432 inches
14b. 321 cm Ο 32.1 m
12 yards = 432 inches
321 cm < 32.1 m
Explanation:
14a. 12 yards Ο 432 inches
1 yard = 36 inches
12 yards = 12×36 = 432 inches
So, 12 yards = 432 inches
14b. 321 cm Ο 32.1 m
100 centimeters = 1 meter
1 centimeter = 0.01 meter
321 centimeters = 321×0.01 meters = 3.21 meters
3.21 < 32.1
So, 321 centimeters < 32.1 meters
Convert Units of Length – Page No. 319
Convert to the given unit.
Question 1.
42 ft = ? yd
_______ yd
Answer:
14yd
Explanation:
42 ft= ?yd
3 feet = 1 yard
1 feet = 1/3 yard
So, 42 feet = 42/3 = 14 yard
So, 42 feet = 14 yards
Question 2.
2,350 m = ? km
_______ km
Answer:
2.350 km
Explanation:
2,350 m = ? km
1 kilometer = 1000 meters
1 meter = 1/1000 kilometers
Then, 2350 meters = 2350/1000 kilometers
2350 meters = 2.350 kilometers
Question 3.
18 ft = ? in.
_______ inches
Answer:
216 inches
Explanation:
18 ft= ? in
1 foot = 12 inches
18 feet = 12×18 = 216 inches
18 feet = 216 inches
Question 4.
289 m = ? dm
_______ dm
Answer:
2890 dm
Explanation:
289 m = ?dm
10 decimeters = 1 meter
289 meters = 289×10 decimeters
So, 289 meters = 2890 decimeters
Question 5.
5 mi = ? yd
_______ yd
Answer:
8,800 yd
Explanation:
1. 5 mi = ? yd
1 mile = 1760 yards
5 miles = 5×1760 = 8800 yards
5 mi = 8,800 yards
Chapter 6 Lesson 1 Answer Key Question 6.
35 mm = ? cm
_______ cm
Answer:
3.5 cm
Explanation:
35 mm = ? cm
1000 millimeters = 1 meter
100 centimeters = 1 meter
So, 1000 millimeters = 100 centimeters
1 millimeter = 100/1000 centimeters
Then, 35 millimeters = 35×100/1000 centimeters = 3.5 centimeters
35 millimeters = 3.5 centimeters
Compare. Write <, >, or =.
Question 7.
1.9 dm _______ 1,900 mm
Answer:
1.9 dm < 1,900 mm
Explanation:
1.9 dm _______ 1,900 mm
10 decimeters = 1 meter
1000 millimeters = 1 meter
So, 10 decimeters = 1000 millimeters
1 decimeter = 100 millimeters
1.9 decimeters = 1.9 x 100 = 190 millimeters
So, 1.9 decimeters = 190 millimeters
So, 1.9 dm < 1900 mm
Question 8.
12 ft _______ 4 yd
Answer:
12 ft = 4 yd
Explanation:
12 ft _______ 4 yd
3 feet = 1 yard
3×4 feet = 12 feet = 1×4 = 4 yard
So, 12 feet = 4 yards
Question 9.
56 cm _______ 56,000 km
Answer:
56 cm < 56,000 km
Explanation:
56 cm _______ 56,000 km
100 centimeters = 1 meter
1 kilometer = 1000 meters
0.01 kilometer = 1 meter
So, 100 centimeters = 0.01 kilometers
1 centimeter = 0.01/100 kilometers
56 centimeters = 56 x 0.01/100 kilometers =0.0056 kilometers
So, 56 cm < 56,000 km
Question 10.
98 in. _______ 8 ft
Answer:
98 in. > 8 ft
Explanation:
98 in. _______ 8 ft
1 foot = 12 inches
8 feet = 8×12 = 96 inches
So, 98 in > 8 feet
Question 11.
64 cm _______ 630 mm
Answer:
64 cm > 630 mm
Explanation:
64 cm _______ 630 mm
1000 millimeters = 1 meter
100 centimeters = 1 meter
So, 100 centimeters = 1000 millimeters
1 centimeter = 10 millimeters
so, 64 centimeters = 64×10 millimeters = 640 millimeters
then, 64 cm > 630 mm
Question 12.
2 mi _______ 10,560 ft
Answer:
2 mi = 10,560 ft
Explanation:
1 mi _______ 10,560 ft
1 mile = 5280 feet
so, 2 miles = 2×5280 = 10560 feet
then, 2 miles = 10,560 feet
Question 13.
The giant swallowtail is the largest butterfly in the United States. Its wingspan can be as large as 16 centimeters. What is the maximum wingspan in millimeters?
_______ mm
Answer:
160 mm
Explanation:
The giant swallowtail is the largest butterfly in the United States. Its wingspan can be as large as 16 centimeters.
100 centimeters = 1 meter
1000 millimeters = 1 meter
So, 100 centimeters = 1000 millimeters
1 centimeters = 10 millimeters
then 16 centimeters = 16×10 millimeters = 160 millimeters
So, giant swallowtail wingspan is 160 millimeters large
Lesson 6 Exit Ticket 6.1 Answer Key Question 14.
The 102nd floor of the Sears Tower in Chicago is the highest occupied floor. It is 1,431 feet above the ground. How many yards above the ground is the 102nd floor?
_______ yd
Answer:
477 yd
Explanation:
The 102nd floor of the Sears Tower in Chicago is the highest occupied floor. It is 1,431 feet above the ground.
3 feet = 1 yard
1 feet = 1/3 yard
Then, 1431 feet = 1431/3 yard = 477 yards
So, the height of the 102nd floor from the ground = 477 yards
Question 15.
Explain why units can be simplified first when measurements are multiplied.
Type below:
____________
Answer:
Units can be simplified first, because if (60 min)/(1 hr) = 1, then I can multiply any measurement by that fraction and not change its value.
Lesson Check – Page No. 320
Question 1.
Justin rides his bicycle 2.5 kilometers to school. Luke walks 1,950 meters to school. How much farther does Justin ride to school than Luke walks to school?
_______ meters
Answer:
550 meters
Explanation:
Justin rides his bicycle 2.5 kilometers to school. Luke walks 1,950 meters to school.
1 kilometer = 1000 meters
Then, 2.5 kilometers = 2.5 x 1000 = 2500 meters
So, Justin rides his bicycle 2500 meters and Luke walks 1950 meters
2500 – 1950 = 550 meters
So, Justin rides more 550 meters than Luke to school
Lesson 6 Practice Problems Answer Key Grade 6 Question 2.
The length of a room is 10 \(\frac{1}{2}\) feet. What is the length of the room in inches?
_______ inches
Answer:
126 inches
Explanation:
1 feet = 12 inches
10 1/2 feet = ?
10 1/2 = 21/2
21/2 × 12 = 21 × 6 = 126
126 inches
Spiral Review
Question 3.
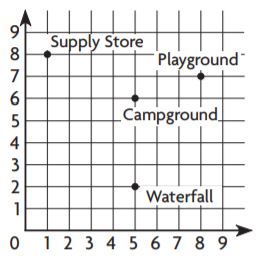
Each unit on the map represents 1 mile. What is the distance between the campground and the waterfall?
_______ miles
Answer:
4 miles
Explanation:
Each unit on the map represents 1 mile
The distance between the campground and the waterfall is 4 units that is 4 miles
Question 4.
On a field trip, 2 vans can carry 32 students. How many students can go on a field trip when there are 6 vans?
_______ students
Answer:
96 students
Explanation:
On a field trip, 2 vans can carry 32 students
So, 1 van can carry the students = 32/2 = 16 students
Then, students can go in 6 vans = 6×16 = 96 students
Question 5.
According to a 2008 survey, \(\frac{29}{50}\) of all teens have sent at least one text message in their lives. What percent of teens have sent a text message?
_______ %
Answer:
58%
Explanation:
From the given information
According to a 2008 survey
29/50 of all teens have sent at least one text message in their lives
Percent of teens have sent a text message = 29/50 x 100 = 58%
So, 58% of teens have sent text messages
Question 6.
Of the students in Ms. Danver’s class, 6 walk to school. This represents 30% of her students. How many students are in Ms. Danver’s class?
_______ students
Answer:
20 students
Explanation:
Of the students in Ms. Danver’s class, 6 walk to school
It represents 30% of her students
That is 30% = 6 students
Then 100% = (100×6)/30 = 20
Total number of students in Ms. Danver’s class = 20 students
Share and Show – Page No. 323
Convert to the given unit.
Question 1.
5 quarts = ? cups
_______ cups
Answer:
20 cups
Explanation:
5 quarts = ? cups
4cups = 1 quart
So, 5 quarts = 5×4 = 20 cups
5 quarts = 20 cups
Question 2.
6.7 liters = ? hectoliters
_______ hectoliters
Answer:
0.067 hectoliters
Explanation:
1.7 liters = ? hectoliters
1 hectoliter= 100 liters
1 liter = 1/100 hectoliters
6.7 liters = 6.7/100 hectoliters = 0.067 hectoliters
Question 3.
5.3 kL = ? L
_______ L
Answer:
5300 L
Explanation:
5.3 kL= ? L
1 Kiloliter = 1000 liters
Then, 5.3 kiloliters = 5.3 x 1000 = 5300 liters
So, 5.3 kL = 5300 L
Question 4.
36 qt = ? gal
_______ gal
Answer:
9 gal
Explanation:
36 qt = ? gal
4 quarts = 1 gallon
So, 36 qts = 9×4 quarts = 9×1 gallons
So, 36 qt = 9 gallons
Convert Units of Capacity Lesson 6.2 Homework Answers Question 5.
5,000 mL = ? cL
_______ cL
Answer:
500 cL
Explanation:
5,000 mL = ?cL
1000 milliliters = 1 liter
100 centiliters = 1 liter
So, 1000 milliliters = 100 centiliters
Then, 5000 milliliters = 5×100 centiliters = 500 centiliters
5000 milliliters = 500 centiliters
On Your Own
Question 6.
It takes 41 gallons of water for a washing machine to wash a load of laundry. How many quarts of water does it take to wash one load?
_______ quarts
Answer:
164 quarts
Explanation:
It takes 41 gallons of water for a washing machine to wash a load of laundry.
41 gallons of water is required for a washing machine to wash a load of laundry
1 gallon = 4 quarts
Then, 41 gallons = 41×4 quarts = 164 quarts
164 quarts of water us required for a washing machine to wash a load of laundry
Question 7.
Sam squeezed 237 milliliters of juice from 4 oranges. How many liters of juice did Sam squeeze?
_______ L
Answer:
0.237 L
Explanation:
Sam squeezed 237 milliliters of juice from 4 oranges
1000 liliters = 1 liter
1 milliliter = 1/1000 liter
237 milliliters = 237/1000 liters
237 milliliters = 0.237 liters
Question 8.
Reason Quantitatively A bottle contains 3.78 liters of water. Without calculating, determine whether there are more or less than 3.78 deciliters of water in the bottle. Explain your reasoning
Type below:
____________
Answer:
Reason Quantitatively A bottle contains 3.78 liters of water
1 liter = 10 deciliters
Then 3.78 liters = 3.78×10 = 37.8 deciliters
So, bottle contains more than 3.78 deciliters of water
Question 9.
Tonya has a 1-quart, a 2-quart, and a 3-quart bowl. A recipe asks for 16 ounces of milk. If Tonya is going to triple the recipe, what is the smallest bowl that will hold the milk?
The _______ bowl
Answer:
The 3 quarts bowl
Explanation:
Tonya has a 1-quart, a 2-quart, and a 3-quart bowl
A recipe asks for 16 ounces of milk
If Tonya triples the recipe, then 1 quart = 3, 2 quart = 6, 3 quart = 9
The smallest bowl is 3 quarts
Practice: Copy and Solve Compare. Write <, >, or =.
Question 10.
700,000 L _______ 70 kL
Answer:
700,000 L > 70 kL
Explanation:
700,000 L _______ 70 kL
1 kiloliter = 1000 liters
Then, 70 kiloliters = 70×1000 liters = 70,000 liters
So, 700,000 liters > 70 kiloliters
Question 11.
6 gal _______ 30 qt
Answer:
6 gal < 30 qt
Explanation:
6 gal _______ 30 qt
4 quarts = 1 gallon
So, 6 gallons = 6×4 = 24 quarts
So, 6 gallons < 30 quarts
Question 12.
54 kL _______ 540,000 dL
Answer:
54 kL = 540,000 dL
Explanation:
54 kL _______ 540,000 dL
1 kiloliter = 1000 liters
1 liter = 10 deciliters
Then, 1000 liters = 10×1000 = 10,000 deciliters
So, 1 kiloliter = 10,000 deciliters
Then, 54 kiloliters = 54×10,000 = 540,000 deciliters
So, 54 kL = 540,000 dL
Lesson 6.2 Answer Key 6th Grade Question 13.
10 pt _______ 5 qt
Answer:
10 pt = 5 qt
Explanation:
10 pt _______ 5 qt
1 pints = 1 quart
then, 10 pints = 2×5 pints = 1×5 quart = 5 quarts
So, 10 pints = 5 quarts
Question 14.
500 mL _______ 50 L
Answer:
500 mL < 50 L
Explanation:
500 mL _______ 50 L
1000 milliliters = 1 liter
Then, 1000/2 milliliters = 500 milliliters = ½ liters= 0.5 liters
So, 500 mL < 50 L
Question 15.
14 c _______ 4 qt
Answer:
14 c < 4 qt
Explanation:
14 c _______ 4 qt
4 cups = 1 quart
1 cup = ¼ quart
Then, 14 cups = 14/4 quarts = 3.5 quarts
So, 14 cups < 4 quarts
Unlock the Problem – Page No. 324
Question 16.
Jeffrey is loading cases of bottled water onto a freight elevator. There are 24 one-pint bottles in each case. The maximum weight that the elevator can carry is 1,000 pounds. If 1 gallon of water weighs 8.35 pounds, what is the maximum number of full cases Jeffrey can load onto the elevator?
a. What do you need to find?
Type below:
____________
Answer:
The maximum number of full cases Jeffrey can load onto the elevator
Question 16.
b. How can you find the weight of 1 case of bottled water? What is the weight?
Type below:
____________
Answer:
Using one-pint bottles and 1 gallon of water weighs 8.35 pounds Information
Explanation:
Question 16.
c. How can you find the number of cases that Jeffrey can load onto the elevator?
Type below:
____________
Answer:
1 US liquid pint is equivalent to 0.125 US liquid gallons.
So, 24 one-pint bottles is equivalent to (24 × 0.125) =3 gallons.
Therefore, one full case of bottled water is equal to 3 gallons.
Now, 1 gallon is equal to 8.35 pounds
And hence, 3 gallons is equal to (8.35 × 3) = 25.05 pounds.
Question 16.
d. What is the maximum number of full cases Jeffrey can load onto the elevator?
_______ cases
Answer:
39 cases
Explanation:
1 US liquid pint is equivalent to 0.125 US liquid gallons.
So, 24 one-pint bottles is equivalent to (24 × 0.125) =3 gallons.
Therefore, one full case of bottled water is equal to 3 gallons.
Now, 1 gallon is equal to 8.35 pounds
And hence, 3 gallons is equal to (8.35 × 3) = 25.05 pounds.
If the maximum weight that the elevator can carry is 1000 pounds, then the maximum number of cases of bottled water that the elevator can carry is ≈ 39
We can not take the number as 40, because then the total weight will become more than 1000 pounds which is not allowed.
Lesson 6 Classwork 6.2 Answer Key Question 17.
Monica put 1 liter, 1 deciliter, 1 centiliter, and 1 milliliter of water into a bowl. How many milliliters of water did she put in the bowl?
_______ milliliters
Answer:
1111 milliliters
Explanation:
Monica put 1 liter, 1 deciliter, 1 centiliter, and 1 milliliter of water into a bowl
1 liter = 1000 milliliters
1 liter = 10 deciliters
so, 10 deciliters = 1000 milliliters
then, 1 deciliter = 100 milliliters
1 liter = 100 centiliters
So, 100 centiliters = 1000 milliliters
Then, 1 centiliter = 10 milliliters
1 liter + 1 deciliter + 1 centiliter + 1 milliliter
= 1000 milliliters + 100 milliliters + 10 milliliters + 1 milliliter
= 1111 milliliters
Monica filled the bowl with 1111 milliliters of water
Question 18.
Select the conversions that are equivalent to 235 liters. Mark all that apply.
Options:
a. 235,000 milliliters
b. 0.235 milliliters
c. 235,000 kiloliters
d. 0.235 kiloliters
Answer:
a. 235,000 milliliters
Explanation:
a. 235,000 milliliters
1000 milliliters = 1 liter
Then, 235×1000 milliliters = 1×235 liters = 235 liters
So, 235,000 milliliters are equivalent to 235 liters
Convert Units of Capacity – Page No. 325
Convert to the given unit.
Question 1.
7 gallons = ? quarts
_______ quarts
Answer:
28 quarts
Explanation:
6 gallons = ? quarts
4 quarts = 1 gallon
then, 7 gallons = 4×7 = 28 quarts
Question 2.
5.1 liters = ? kiloliters
_______ kiloliters
Answer:
0.0051 kiloliters
Explanation:
5.1 liters = ? kiloliters
1 kiloliter = 1000 liters
So, 1 liter = 1/1000 kiloliter
Then, 5.1 liters = 5.1/1000 kiloliters
5.1 liters = 0.0051 kiloliters
Question 3.
20 qt = ? gal
_______ gal
Answer:
5 gal
Explanation:
20 t = ? gal
4 quarts = 1 gallon
Then, 4×5 quarts = 1×5 gallons
That is 20 quarts = 5 gallons
Question 4.
40 L = ? mL
_______ mL
Answer:
40,000 mL
Explanation:
40 L = ? mL
1000 milliliters = 1 liter
Then, 40 liters = 40×1000 milliliters = 40,000 milliliters
40 L = 40,000 mL
Question 5.
33 pt = ? qt ? pt
_______ qt _______ pt
Answer:
33/2 quarts = 16.5 quarts
Explanation:
33 pt= ?qt ? pt
1 pints = 1 quart
1 pint = ½ quart
then, 33 pint = 33/2 quarts = 16.5 quarts
Question 6.
29 cL = ? daL
_______ daL
Answer:
0.029 daL
Explanation:
29 cL = ? daL
100 centiliters = 1 liter
1 dekaliter = 10 liters
So, 1 liter = 1/10 dekaliters
Then, 100 centiliters = 1/10 dekaliters
1 centiliter = 1/1000 dekaliters
then, 29 centiliters = 29/1000 dekaliters = 0.029 dekaliters
29 cL = 0.029 daL
Lesson 6 Problem Set 6.2 Answer Key Question 7.
7.7 kL = ? cL
_______ cL
Answer:
7,70,000 cL
Explanation:
6.7 kL = ? cL
1 kiloliter = 1000 liters
100 centiliters = 1 liter
So, 1000 liters = 100×1000 centiliters = 1,00,000 centiliters
Then, 1 kiloliter = 1,00,000 centiliters
Then, 7.7 kiloliters = 7.7 x 1,00,000 centiliters = 7,70,000 centiliters
Question 8.
24 fl oz = ? pt ? c
_______ pt _______ c
Answer:
3/2 pt and 3 cups
Explanation:
24 floz= ?pt ? c
6 fluids ounces = 1 cup
then, 24 fluid ounces = 8×3 = 1×3 cups = 3 cups
1 cups = 1 pint
then, 1 cup = ½ pint
then, 3 cups = 3/2 pint
so, 24 fluids ounces = 3/2 pint and 3 cups
Problem Solving
Question 9.
A bottle contains 3.5 liters of water. A second bottle contains 3,750 milliliters of water. How many more milliliters are in the larger bottle than in the smaller bottle?
_______ mL
Answer:
250 mL
Explanation:
A bottle contains 3.5 liters of water. A second bottle contains 3,750 milliliters of water.
A bottle contains 3.5 liters of water
A second bottle contains 3,750 milliliters of water
1000 milliliters = 1 liter
Then, 3.5 liters = 3.5×1000 = 3500 milliliters
So, 3750 – 3500 = 250 milliliters
250 milliliters of water is more than in the larger bottle than the smaller bottle
Question 10.
Arnie’s car used 100 cups of gasoline during a drive. He paid $3.12 per gallon for gas. How much did the gas cost?
$ _______
Answer:
$19.5
Explanation:
Arnie’s car used 100 cups of gasoline during a drive. He paid $3.12 per gallon for gas.
Arnie’s car used 100 cups of gasoline during a drive
He paid $3.12 per gallon for gas
1 gallon = 4 quarts
1 quart = 4 cups
then, 4 quarts = 4×4 cups = 16 cups
So, 1 gallon = 16 cups
Then, 1 cup = 1/16 gallons
Then, 100 cups = 100/16 gallons = 6.25 gallons
Total gas cost = $3.12 x 6.25 = $19.5
Question 11.
Explain how units of length and capacity are similar in the metric system.
Type below:
____________
Answer:
In the metric system, The unit of length is a meter (m) and the unit of capacity is the liter (L)
Lesson Check – Page No. 326
Question 1.
Gina filled a tub with 25 quarts of water. What is this amount in gallons and quarts?
_______ gallons _______ quart
Answer:
6 gallons and 1 quart
Explanation:
Gina filled a tub with 25 quarts of water
4quarts = 1 gallon
1 quart = ¼ gallon
25 quarts = 25/4 gallon = 6 gallons and 1 quart
Gina filled a tub with 6 gallons and 1 quart
Question 2.
Four horses are pulling a wagon. Each horse drinks 45,000 milliliters of water each day. How many liters of water will the horses drink in 5 days?
_______ liters
Answer:
900 liters
Explanation:
Four horses are pulling a wagon
Each horse drinks 45,000 milliliters of water each day
Then, four horses drinks 4×45,000 milliliters = 1,80,000
1000 milliliters = 1 liter
Then, 180×1000 = 1,80,000 milliliters = 180 liters
180 x 5 = 900 liters
Horses drink 900 liters of water in 5 days
Spiral Review
Question 3.
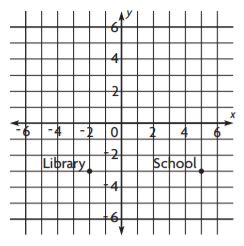
The map shows Henry’s town. Each unit represents 1 kilometer. After school, Henry walks to the library. How far does he walk?
_______ kilometers
Answer:
7 kilometers
Explanation:
The map shows Henry’s town. Each unit represents 1 kilometer. After school, Henry walks to the library.
Each unit represents 1 kilometer
After school, Henry walks to the library
Distance between school and library = 7 kilometers
So, henry walks 7 kilometers from school to library
Question 4.
An elevator travels 117 feet in 6.5 seconds. What is the elevator’s speed as a unit rate?
_______ feet per second
Answer:
18 feet per second
Explanation:
An elevator travels 117 feet in 6.5 seconds.
The elevator’s speed as a unit rate = 117/6.5 = 18 feet per second
Question 5.
Julie’s MP3 player contains 860 songs. If 20% of the songs are rap songs and 15% of the songs are R&B songs, how many of the songs are other types of songs?
_______ songs
Answer:
559 songs
Explanation:
Julie’s MP3 player contains 860 songs
20% of the songs are rap songs = 860×20/100 = 172
15% of the songs are R & B songs = 860×15/100 = 129
Other types of songs = 860 – 172-129 = 559
Question 6.
How many kilometers are equivalent to 3,570 meters?
_______ kilometers
Answer:
3.57 kilometers
Explanation:
1 kilometer = 1000 meters
then,1 meter = 1/1000 kilometer
So, 3570 meters = 3570/1000 kilometer
3570 meters = 3.57 kilometers
Share and Show – Page No. 329
Convert to the given unit.
Question 1.
9 pounds = ? ounces
_______ ounces
Answer:
144 ounces
Explanation:
6 pounds = ? ounces
1 pound = 16 ounces
then, 9 pounds = 9×16 ounces = 144 ounces
Question 2.
3.77 grams = ? dekagram
_______ dekagram
Answer:
0.377 dekagram
Explanation:
3.77 grams = ? dekagram
1 dekagram = 10 grams
1 gram = 1/10 dekagram
Then, 3.77 grams = 3.77/10 dekagram = 0.377 dekagram
So, 3.77 grams = 0.377 dekagram
Question 3.
Amanda’s computer weighs 56 ounces. How many pounds does it weigh?
_______ pounds
Answer:
3.5 pounds
Explanation:
Amanda’s computer weighs 56 ounces
1 pound = 16 ounces
then, 1 ounce = 1/16 pound
So, 56 ounces = 56/16 pounds = 3.5 pounds
Question 4.
A honeybee can carry 40 mg of nectar. How many grams of nectar can a honeybee carry?
_______ grams
Answer:
0.04 grams
Explanation:
A honeybee can carry 40 mg of nectar.
1000 milligrams = 1 gram
1 milligram = 1/1000 grams
Then, 40 milligrams = 40/1000 grams = 0.04 grams
So, the honeybee can carry 0.04 grams of nectar
On Your Own
Convert to the given unit.
Question 5.
4 lb = ? oz
_______ oz
Answer:
64 oz
Explanation:
4lb = ?oz
1 pound (lb) = 16 ounces
then, 4 pounds = 4×16 ounces = 64 ounces
Question 6.
7.13 g = ? cg
_______ cg
Answer:
713 cg
Explanation:
7.13g = ? cg
100 centigrams = 1 gram
Then, 7.13 grams = 100×7.13 = 713 centigrams
So, 7.13 grams = 713 centigrams
Question 7.
3 T = ? lb
_______ lb
Answer:
6000 lb
Explanation:
3T = ?lb
1 ton = 2000 pounds (lb)
then, 3 tons = 3×2000 = 6000 pounds (lb)
Question 8.
The African Goliath frog can weigh up to 7 pounds. How many ounces can the Goliath frog weigh?
_______ ounces
Answer:
112 ounces
Explanation:
The African Goliath frog can weigh up to 7 pounds.
1 pound = 16 ounces
7 pounds = 7×16 = 112 pounds
So, the Goliath frog can weigh up to 112 pounds
Question 9.
The mass of a standard hockey puck must be at least 156 grams. What is the minimum mass of 8 hockey pucks in kilograms?
_______ kg
Answer:
1.248 kg
Explanation:
The mass of a standard hockey puck must be at least 156 grams.
1 kilogram = 1000 grams
1 gram = 1/1000 kilogram
then, 156 grams = 156/1000 kilograms = 0.156 kilograms
mass of a hockey puck is 0.156 kilograms
then, the mass of 8 hockey pucks is 8×0.156 = 1.248 kilograms
Practice: Copy and Solve Compare. Write <, >, or =.
Question 10.
250 lb _______ 0.25 T
Answer:
250 lb < 0.25 T
Explanation:
250 lb_______ 0.25 T
1 ton = 2000 pounds(lb)
then, 0.25 tons =0.25×2000 = 500 pounds = 500lb
So, 250 lb < 0.25 T
Question 11.
65.3 hg _______ 653 dag
Answer:
65.3 hg = 653 dag
Explanation:
65.3 hg _______ 653 dag
1 hectogram = 100 grams
Then, 65.3 hectograms = 65.3×100 = 6530 grams
1 dekagram = 10 grams
then, 653 dekagram = 6530 grams
So, 65.3 hectogram = 653 dekagram
Question 12.
5 T _______ 5,000 lb
Answer:
5 T > 5,000 lb
Explanation:
5 T _______ 5,000 lb
1 ton = 2000 pounds (lb)
5 tons = 5×2000 lb = 10,000 lb
Then, 5 T > 5000 lb
Question 13.
Masses of precious stones are measured in carats, where 1 carat = 200 milligrams. What is the mass of a 50-dg diamond in carats?
_______ carats
Answer:
25 carats
Explanation:
Masses of precious stones are measured in carats, where 1 carat = 200 milligrams.
1 carat = 200 milligrams
6 decigrams = 1 gram
1000 milligrams = 1 gram
So, 10 decigrams = 1000 milligrams
Then, 1 decigram = 100 milligram
2 decigrams = 200 milligrams = 1 carat
then, 50 decigrams = 2×25 decigrams = 25×200 milligrams = 25 carats
Problem Solving + Applications – Page No. 330
Use the table for 14–17.

Question 14.
Express the weight range for bowling balls in pounds.
_______ lb
Answer:
16 lb
Explanation:
Weight range for bowling balls = 160 to 256 ounces
1 pound = 16 ounces
So, 1 ounce = 1/16 pounds
Then, 160 ounces = 160/16 pounds = 10 pounds
256 ounces = 256/16 pounds = 16 pounds
So, the weight range for bowling balls is 10 to 16 pounds
Question 15.
How many more pounds does the heaviest soccer ball weigh than the heaviest baseball? Round your answer to the nearest hundredth.
_______ lb
Answer:
0.68 lb
Explanation:
The heaviest soccer ball weight = 16 ounces
1 pound = 16 ounces
Heaviest baseball weight = 5.25 ounces
1 pound = 16 ounces
1 ounce = 1/16 pounds
then, 5.25 ounces = 5.25/16 = 0.32 pounds
difference between soccer ball and baseball weight = 1 – 0.32 = 0.68 pounds
So, the soccer ball weight is 0.68 pounds more than the weight of the baseball.
Lesson 6.3 Answer Key 6th Grade Question 16.
A manufacturer produces 3 tons of baseballs per day and packs them in cartons of 24 baseballs each. If all of the balls are the minimum allowable weight, how many cartons of balls does the company produce each day?
_______ cartons
Answer:
800 cartons
Explanation:
3 tons = 6000 lbs.
Baseball = 5 ounces
16 ounces in 1 pound
6000 × 16 = 96,000
96,000/5 = 19,200
19,200/24 = 800
Question 17.
Communicate Explain how you could use mental math to estimate the number of soccer balls it would take to produce a total weight of 1 ton.
Type below:
____________
Answer:
Soccer balls range from 14 to 16 ounces
1 ton = 2000 pounds
then, 1 pound = 1/2000 tons
1 pound = 16 ounces
So, 16 ounces = 1/2000 tons = 0.0005 tons
1 ounce = 1/32000 tons
then, 14 ounces = 14/32000 tons =0.0004375 tons
So, the range of soccer balls is 0.0005 to 0.0004375 tons
Question 18.
The Wilson family’s newborn baby weighs 84 ounces. Choose the numbers to show the baby’s weight in pounds and ounces.
_______ pounds and _______ ounces
Answer:
5 pounds and 4 ounces
Explanation:
The Wilson family’s newborn baby weighs 84 ounces
1 pound = 16 ounces
then, 1 ounce = 1/16 pounds
So, 84 ounces = 84/16 pounds = 5 pounds and 4 ounces
Convert Units of Weight and Mass – Page No. 331
Convert to the given unit.
Question 1.
5 pounds = ? ounces
_______ ounces
Answer:
80 ounces
Explanation:
5 pounds = ? ounces
1 pound = 16 ounces
Then, 5 pounds = 5×16 = 80 ounces
So, 5 pounds = 80 ounces
Question 2.
2.36 grams = ? hectograms
_______ hectograms
Answer:
0.0236 hectograms
Explanation:
1.36 grams = ? hectograms
1 hectogram = 100 grams
1 gram = 1/100 hectograms
then, 2.36 grams = 2.36/100 hectograms = 0.0236 hectograms
So, 2.36 grams = 0.0236 hectograms
Question 3.
30 g = ? dg
_______ dg
Answer:
300 dg
Explanation:
29 g = ? dg
10 decigrams = 1 gram
then, 30 grams = 30×10 decigrams = 300 decigrams
30 grams = 300 decigrams
Question 4.
17.2 hg = ? g
_______ g
Answer:
1720 g
Explanation:
17.2 hg = ? g
1 hectogram = 100 grams
Then, 17.2 hectograms = 17.2×100 = 1720 grams
So, 17.2 hectograms = 1720 grams
Question 5.
400 lb = ? T
_______ T
Answer:
0.2 T
Explanation:
1. 400 lb = ? T
1 ton = 2000 pounds (lb)
400 lb = 2000/5 pounds (lb) = 1/5 tons
So, 400 lb = 0.2 tons
Question 6.
38,600 mg = ? dag
_______ dag
Answer:
3.86 dag
Explanation:
38,600 mg = ? dag
1000 milligrams = 1 gram
1 dekagram = 10 grams
So, 1 gram = 1/10 dekagram
Then, 1000 milligrams = 1/10 dekagrams
1 milligram = 1/10,000 dekagrams
So, 38,600 milligrams = 38,600/10,000 = 3.86 dekagrams
38,600 milligrams = 3.86 dekagrams
Question 7.
87 oz = ? lb ? oz
_______ pounds _______ ounces
Answer:
5 pounds and 7 ounces
Explanation:
87 oz = ? lb ? oz
1 pound = 16 ounces
1 ounce = 1/16 pounds
then, 87 ounces = 87/16 pounds
87 ounces = 5 pounds and 7 ounces
Question 8.
0.65 T = ? lb
_______ lb
Answer:
1300 lb
Explanation:
0.65 T = ?lb
1 ton = 2000 pounds
Then, 0.65 tons = 0.65×2000 = 1300 pounds
0.65 T = 1300 lb
Problem Solving
Question 9.
Maggie bought 52 ounces of swordfish selling for $6.92 per pound. What was the total cost?
$ _______
Answer:
$22.49
Explanation:
Maggie bought 52 ounces of swordfish selling for $6.92 per pound.
Maggie bought 52 ounces of swordfish selling for $6.92 per pound
1 pound = 16 ounces
1 ounce = 1/16 pounds
then, 52 ounces = 52/16 pounds = 3.25 pounds
1 pound cost = $6.92
then, 3.25 pounds cost = $6.92 x 3.25 = $22.49
So, the cost for swordfish is $22.49
Question 10.
Three bunches of grapes have masses of 1,000 centigrams, 1,000 decigrams, and 1,000 grams, respectively. What is the total combined mass of the grapes in kilograms?
_______ kg
Answer:
1.11 kg
Explanation:
Three bunches of grapes have masses of 1,000 centigrams, 1,000 decigrams, and 1,000 grams, respectively.
Three bunches of grapes have masses of 1,000 centigrams, 1,000 decigrams, and 1,000 grams
100 centigrams = 1 gram
then, 1000 centigrams = 10×100 centigrams = 10 grams
1 kilogram = 1000 grams
So, 1 gram = 1/1000 kilograms
Then, 10 grams = 10/1000 = 1/100 kilograms = 0.01 kilograms
10 decigrams = 1 gram
then, 100×10 decigrams = 100×1 gram = 100 grams
1000 grams = 1 kilogram
Then, 100 grams = 1/10 kilograms = 0.1 kilograms
1000 grams = 1 kilogram
Total weight of the grapes = 1 + 0.1 + 0.01 = 1.11 kilograms
Question 11.
Explain how you would find the number of ounces in 0.25T.
Type below:
____________
Answer:
number of ounces in 0.25T
1 ton = 2000 pounds
then, 1 pound = 1/2000 tons
1 pound = 16 ounces
so, 16 ounces = 1/2000 tons
then, 1 ton = 16×2000 ounces = 32000 ounces
So, 0.25 tons = 0.25×32000 ounces = 8000 ounces
8000 ounces = 0.25 T
Lesson Check – Page No. 332
Question 1.
The mass of Denise’s rock sample is 684 grams. The mass of Pauline’s rock sample is 29,510 centigrams. How much greater is the mass of Denise’s sample than Pauline’s sample?
_______ centigrams
Answer:
38900 centigrams
Explanation:
The mass of Denise’s rock sample is 684 grams
The mass of Pauline’s rock sample is 29,510 centigrams
100 centigrams = 1 gram
1 centigram = 1/100 gram
then, 29,510 centigrams = 29,510/100 grams = 295.1 grams
So, the mass of Pauline’s rock sample is 295.1 grams
By comparing Denise’s rock sample with Pauline’s rock sample
684 – 295 = 389
The mass of Denise’s rock sample is 389 grams more than the mass of Pauline’s rock sample
389 grams = 38900 centigrams
Solving Conversion Problems Home Link 6.3 Answer Key Question 2.
A sign at the entrance to a bridge reads: Maximum allowable weight 2.25 tons. Jason’s truck weighs 2,150 pounds. How much additional weight can he carry?
_______ pounds
Answer:
2,350 pounds
Explanation:
A sign at the entrance to a bridge reads: Maximum allowable weight 2.25 tons
Jason’s truck weighs 2,150 pounds
1 ton = 2000 pounds
then, 2.25 tons = 2.25×2000 = 4500 pounds
So, maximum allowable weight = 4500 pounds
4500 – 2150 = 2350
So, Jason can carry an additional 2350 pounds’ of weight
Spiral Review
Question 3.
There are 23 students in a math class. Twelve of them are boys. What is the ratio of girls to total number of students?
Type below:
____________
Answer:
11 : 23
Explanation:
There are 23 students in a math class. Twelve of them are boys.
Number of students in a math class = 23
Number of boys in a class = 12
Number of girls in a class = 23-12 = 11
Then, the ratio of girls to the total number of students = 11/23
Question 4.
Miguel hiked 3 miles in 54 minutes. At this rate, how long will it take him to hike 5 miles?
_______ minutes
Answer:
90 minutes
Explanation:
Miguel hiked 3 miles in 54 minutes.
Then, time for 5 miles = 5×54/3 = 90 minutes
So, Miguel hikes 5 miles in 90 minutes
Question 5.
Marco borrowed $150 from his brother. He has paid back 30% so far. How much money does Marco still owe his brother?
$ _______
Answer:
$60
Explanation:
Marco borrowed $150 from his brother
He has paid back 30% of amount = 30/100 (150) = $45
Remaining amount = 150 -45 = 60
So, still $60 amount Marco need to give his brother
Question 6.
How many milliliters are equivalent to 2.7 liters?
_______ milliliters
Answer:
2,700 milliliters
Explanation:
2.7 liters
1000 milliliters = 1 liter
Then, 2.7 liters = 2.7 x 1000 = 2700 milliliters
So, 2,700 milliliters are equivalent to 2.7 liters
Mid-Chapter Checkpoint – Vocabulary – Page No. 333
Choose the best term from the box to complete the sentence.

Question 1.
A _____ is a rate in which the two quantities are equal, but use different units.
Type below:
____________
Answer:
Conversion factor
Question 2.
_____ is the amount a container can hold.
Type below:
____________
Answer:
Capacity
Concepts and Skills
Convert units to solve.
Question 3.
A professional football field is 160 feet wide. What is the width of the field in yards?
_____ \(\frac{□}{□}\) yd
Answer:
53\(\frac{1}{3}\) yd
Explanation:
A professional football field is 160 feet wide
3feet = 1 yard
Then, 160 feet = 160/3 = 53.33
So, the width of football field is 53.33 yards
160/3 = 53 1/3
Question 4.
Julia drinks 8 cups of water per day. How many quarts of water does she drink per day?
_____ quarts
Answer:
2 quarts
Explanation:
Julia drinks 8 cups of water per day.
4 cups = 1 quart
Then, 8 cups = 8/4 = 2 quarts
So, Julia drinks 2 quarts of water per day
Question 5.
The mass of Hinto’s math book is 4,458 grams. What is the mass of 4 math books in kilograms?
_____ kilograms
Answer:
17.832 kilograms
Explanation:
The mass of Hinto’s math book is 4,458 grams
1kilogram = 1000 grams
Then, 4,458 grams = 4,458/1000 = 4.458 kilograms
Then, the mass of 4 math books = 4×4.458 = 17.832 kilograms
The mass of 4 math books is 17.832 kilograms
Question 6.
Turning off the water while brushing your teeth saves 379 centiliters of water. How many liters of water can you save if you turn off the water the next 3 times you brush your teeth?
_____ liters
Answer:
11.37 liters
Explanation:
Turning off the water while brushing your teeth saves 379 centiliters of water
100centiliters = 1 liter
Then, 379 centiliters = 379/100 = 3.79 liters
if you turn off the water the next 3 times = 3×3.79 liters = 11.37 liters
So, you can save 11.37 liters of water when you turn off the water for 3 times
Convert to the given unit.
Question 7.
34.2 mm = ? cm
_____ cm
Answer:
3.42 cm
Explanation:
34.2 mm = ? cm
1000 millimeters = 1 meter
100centimeters = 1 meter
so, 1000 millimeters = 100 centimeters
then, 10 millimeters = 1 centimeter
then, 34.2 millimeters = 34.2/10 = 3.42 centimeters
So, 34.2 mm = 3.42 cm
Question 8.
42 in. = ? ft
_____ \(\frac{□}{□}\) ft
Answer:
3\(\frac{1}{2}\) ft
Explanation:
41 in. = ? ft
12 inches = 1 foot
then, 42 inches = 42/12 = 3.5 feet
So, 42 in = 3.5 ft
42/12 = 3 1/2
Question 9.
1.4 km = ? hm
_____ hm
Answer:
140 hm
Explanation:
1.4 km = ? hm
1 kilometer = 1000 meters
1 hectometer = 100 meters
So, 1 meter = 0.001 kilometers
1 meter = 0.01 hectometers
Now, 0.001 kilometer = 0.01 hectometer
That is 0.1 kilometer = 1 hectometer
Then, 1.4 kilometer = 1.4/0.1 = 140 hectometers
So, 1.4 km = 140 hm
Question 10.
4 gal = ? qt
_____ qt
Answer:
16 qt
Explanation:
4gal = ?qt
1gallon = 4 quarts
Then, 4 gallons = 4×4 = 16 quarts
So, 4 gal = 16 qt
Question 11.
53 dL = ? daL
_____ daL
Answer:
0.53 daL
Explanation:
53 dL = ? daL
10deciliters = 1 liter
1 dekaliter = 10 liters that is 0.1 dekaliters = 1 liter
So, 10 dL = 0.1 daL
Then, 53 dL = 53×0.1/10 =0.53 daL
So, 53 dL = 0.53 daL
Question 12.
28 c = ? pt
_____ pt
Answer:
14 pt
Explanation:
28 c = ?pt
1 cups = 1pint
then, 28 cups = 28/2 = 14 pints
So, 28 c = 14 pt
Page No. 334
Question 13.
Trenton’s laptop is 32 centimeters wide. What is the width of the laptop in decimeters?
_____ dm
Answer:
3.2 dm
Explanation:
Trenton’s laptop is 32 centimeters wide.
100 centimeters = 1 meter
10decimeters = 1 meter
So, 100 centimeters = 10 decimeters
Then, 32 centimeters = 32×10/100 = 3.2 decimeters
So, the width of the laptop is 3.2 decimeters
Question 14.
A truck is carrying 8 cars weighing an average of 4,500 pounds each. What is the total weight in tons of the cars on the truck?
_____ tons
Answer:
18 tons
Explanation:
A truck is carrying 8 cars weighing an average of 4,500 pounds each.
So, total weight = 8 x 4500 pounds = 36,000 pounds
2000 pounds = 1 ton
Then, 36,000 pounds = 36,000 / 2000 = 18 tons
So, total weight of the cars in truck is 18 tons
Question 15.
Ben’s living room is a rectangle measuring 10 yards by 168 inches. By how many feet does the length of the room exceed the width?
_____ feet
Answer:
16 feet
Explanation:
Ben’s living room is a rectangle measuring 10 yards by 168 inches.
12inches = 1 foot
Then, 168 inches = 168/12 = 14 feet
1 yard = 3 feet
then, 10 yards = 10×3 = 30 feet
30-14 = 16 feet
So, the length of the room exceeds 16 feet in width
Grade 6 Unit 6 Answer Key Question 16.
Jessie served 13 pints of orange juice at her party. How many quarts of orange juice did she serve?
_____ quarts
Answer:
6.5 quarts
Explanation:
Jessie served 13 pints of orange juice at her party
1 pints = 1 quart
then, 13 pints = 13/2 = 6.5 quarts
So, Jessie served 6.5 quarts of orange juice at her party
Question 17.
Kaylah’s cell phone has a mass of 50,000 centigrams. What is the mass of her phone in grams?
_____ grams
Answer:
500 grams
Explanation:
Kaylah’s cell phone has a mass of 50,000 centigrams
100 centigrams = 1 gram
then, 50,000 centigrams = 50,000/100 = 500 grams
So, the mass of Kaylah’s phone is 500 grams
Share and Show – Page No. 337
Question 1.
A dripping faucet leaks 12 gallons of water per day. How many gallons does the faucet leak in 6 days?
_____ gallons
Answer:
72 gallons
Explanation:
A dripping faucet leaks 12 gallons of water per day
Then, faucet leaks how many gallons of water per 6 days = 12 x 6 = 72 gallons
Question 2.
Bananas sell for $0.44 per pound. How much will 7 pounds of bananas cost?
$ _____
Answer:
$3.08
Explanation:
Bananas sell for $0.44 per pound
1 pound banana cost is $0.44
then, 7 pounds bananas cost is = 7 x 0.44 = $3.08
Question 3.
Grizzly Park is a rectangular park with an area of 24 square miles. The park is 3 miles wide. What is its length in miles?
_____ miles
Answer:
8 miles
Explanation:
Grizzly Park is a rectangular park with an area of 24 square miles
The park is 3 miles wide
Rectangular park area = length x breadth
That is 24 = 3 x b
So, breadth = 8 miles
The rectangular park length is 8 miles
On Your Own
Multiply or divide the quantities.
Question 4.
\(\frac{24 \mathrm{kg}}{1 \mathrm{min}}\) × 15 min
_____ kg
Answer:
6 kg
Explanation:
24kg1min × 15 min
24 kg / 1min x 15 min
60 min = 1 hour
Then, 15 min = 15/60 = ¼ hours
24 kg x 1/ 4 = 6 kg
Question 5.
216 sq cm÷8 cm
_____ cm
Answer:
27 cm
Explanation:
216 sq cm ÷ 8 cm
216 sq cm/ 8 cm = 27 cm
Question 6.
\(\frac{17 \mathrm{L}}{1 \mathrm{hr}}\) × 9 hr
_____ L
Answer:
153 L
Explanation:
17L1hr x 9 hr
17L/1hr x 9 hr = 153 L
Question 7.
The rectangular rug in Marcia’s living room measures 12 feet by 108 inches. What is the rug’s area in square feet?
_____ square feet
Answer:
108 square feet
Explanation:
The rectangular rug in Marcia’s living room measures 12 feet by 108 inches
1 foot = 12 inches
108 inches = 108/12 = 9 feet
12 x 9 = 108 square feet
Are of rug is 108 square feet
Question 8.
Make Sense of Problems A box-making machine makes cardboard boxes at a rate of 72 boxes per minute. How many minutes does it take to make 360 boxes?
_____ minutes
Answer:
5 minutes
Explanation:
A box-making machine makes cardboard boxes at a rate of 72 boxes per minute
Then, time for 360 boxes = 360/72 = 5 minutes
So, it takes 5 minutes’ time to make 360 boxes
Question 9.
The area of an Olympic-size swimming pool is 1,250 square meters. The length of the pool is 5,000 centimeters. Select True or False for each statement.
9a. The length of the pool is 50 meters.
9b. The width of the pool is 25 meters.
9c. The area of the pool is 1.25 square kilometers
9a. ____________
9b. ____________
9c. ____________
Answer:
9a. True
9b. True
9c. True
Explanation:
The area of an Olympic-size swimming pool is 1,250 square meters
The length of the pool is 5,000 centimeters
100centimeters = 1meter
Then, 5000 centimeters = 5000/100 = 50 meters
Areas of the swimming pool = length x width
1250 square meters = 50 length x 25 width
Then, width = 25 meters
1000 meters = 1 kilometer
then, 1250 square meters = 1250/1000 = 1.25 square meters
Make Predictions – Page No. 338
A prediction is a guess about something in the future. A prediction is more likely to be accurate if it is based on facts and logical reasoning.
The Hoover Dam is one of America’s largest producers of hydroelectric power. Up to 300,000 gallons of water can move through the dam’s generators every second. Predict the amount of water that moves through the generators in half of an hour.

Use what you know about transforming units to make a prediction.
You know the rate of the water through the generators, and you are given an amount of time. Rate of flow:
\(\frac{300,000 \text { gallons }}{1 \text { sec }}\); time: \(\frac{1}{2}\) hr
You want to find the amount of water. Amount of water : ? gallons
Convert the amount of time to seconds to match the units in the rate. \(\frac{1}{2}\) hr=30 min
Multiply the rate by the amount of time to find the amount of water. \(\frac{300,000 \text { gallons }}{1 \mathrm{sec}} \times \frac{1,800 \mathrm{sec}}{1}\) = 540,000,000 gal
So, a good prediction of the amount of water that moves through the generators in half of an hour is 540,000,000 gallons.
Transform units to solve.
Question 10.
An average of 19,230 people tour the Hoover Dam each week. Predict the number of people touring the dam in a year.
_____ people
Answer:
999,960 people
Explanation:
An average of 19,230 people tour the Hoover Dam each week
Number of weeks per year = 52
Then, total number of people tour the hoover dam in the year = 52 x 19, 230 = 999,960
So, 999,960 people touring the hoover dam per year
Question 11.
The Hoover Dam generates an average of about 11,506,000 kilowatt-hours of electricity per day. Predict the number of kilowatt-hours generated in 7 weeks.
_____ kilowatt-hours
Answer:
563,794 kilowatt-hours
Explanation:
The Hoover Dam generates an average of about 11,506,000 kilowatt-hours of electricity per day
1 week = 7 days
7weeks = 7 × 7 = 49 days
Then, Hoover Dam generated electricity per 7 weeks = 49 × 11,506,000 = 563,794,000
So, the total number of kilowatt-hours generated in 7 weeks by the Hoover Dam is 563,794,000
Transform Units – Page No. 339
Multiply or divide the quantities.
Question 1.
\(\frac{62 \mathrm{g}}{1 \mathrm{day}}\) × 4 days
_____ g
Answer:
248 g
Explanation:
62g1day × 4 days
62 g÷1 day × 4 days
Then, 62 g × 4 = 248 g
Question 2.
322 sq yd ÷ 23 yd
_____ yd
Answer:
14 yd
Explanation:
322 sqyd ÷ 23 yd
322 sqyd / 23 yd = 14 sq
Question 3.
\(\frac{128 \mathrm{kg}}{1 \mathrm{hr}}\) × 10 hr
_____ kg
Answer:
1,280 kg
Explanation:
128kg1hr × 10 hr
128 kg/1hr * 10hr
So, 1,280 kg
Question 4.
136 sq km ÷ 8 km
_____ km
Answer:
17 km
Explanation:
136 sq km ÷ 8 km
136 sq km / 8 km
136 sq / 8 = 17
Question 5.
\(\frac{88 \mathrm{lb}}{1 \mathrm{day}}\) × 12 days
_____ lb
Answer:
1,056 lb
Explanation:
88lb1day × 12 days
88lb / 1 day × 12days
That is 88lb × 12 = 1,056 lb
Question 6.
154 sq mm ÷ 11 mm
_____ mm
Answer:
14 mm
Explanation:
154 sq mm ÷ 11 mm
154 sq / 11 = 14
Question 7.
\(\frac{\$ 150}{1 \mathrm{sq} \mathrm{ft}}\) × 20 sq ft
$ _____
Answer:
$30,020 sqft
Explanation:
$1501sqft × 20 sqft
Multiplication of 1501 and 20 is
30,020
That is $1501sqft x 20 sqft = $30,020 sqft
Question 8.
234 sq ft÷18 ft
_____ ft
Answer:
13 ft
Explanation:
234 sq ft÷18 ft
234 sq / 18 = 13
Problem Solving
Question 9.
Green grapes are on sale for $2.50 a pound. How much will 9 pounds cost?
$ _____
Answer:
$22.5
Explanation:
Green grapes are on sale for $2.50 a pound
1 pound = $2.50
then, 9 pounds cost = 9*$2.50 = $22.5
green grapes cost for 9 pounds is $22.5
Question 10.
A car travels 32 miles for each gallon of gas. How many gallons of gas does it need to travel 192 miles?
_____ gallons
Answer:
6 gallons
Explanation:
A car travels 32 miles for each gallon of gas
Then, 192 miles is = 192/ 32 = 6 gallons of gas
So, total 6 gallons of gas is required to travel 192 miles
Question 11.
Write and solve a problem in which you have to transform units. Use the rate 45 people per hour in your question.
Type below:
____________
Answer:
A fast-food restaurant is trying to find out how many customers they had in the last 3 hours, and they know they get 45 people per hour. How many customers were served in the last 3 hours? The answer is 135 people.
Lesson Check – Page No. 340
Question 1.
A rectangular parking lot has an area of 682 square yards. The lot is 22 yards wide. What is the length of the parking lot?
_____ yards
Answer:
31 yards
Explanation:
A rectangular parking lot has an area of 682 square yards
Width of the parking lot = 22 yards wide
Area = length *width
682 square yards= length * 22 yards wide
So, length = 682 square yards / 22 yards = 31 yards
Then, length of the parking lot = 31 yards
Question 2.
A machine assembles 44 key chains per hour. How many key chains does the machine assemble in 11 hours?
_____ key chains
Answer:
484 key chains
Explanation:
A machine assembles 44 key chains per hour
Then, the machine assembles key chains per 11 hours = 11*44 = 484 key chains
So, the machine assembles totally 484 key chains in 11 hours
Spiral Review
Question 3.
Three of these ratios are equivalent to \(\frac{8}{20}\). Which one is NOT equivalent?
\(\frac{2}{5} \quad \frac{12}{24} \quad \frac{16}{40} \quad \frac{40}{100}\)
\(\frac{□}{□}\)
Answer:
\(\frac{8}{20}\)
Explanation:
The below mentioned ratios are equivalent to 8/20
i. 2/5
Multiply the numerator and denominator with 4
That is (2*4)/(5*4) = 8/20
ii. 12/24
Divide the numerator and denominator with 6
That is (12÷6)/(24÷6) = 2/4
Now, multiply the numerator and denominator with 4
That is (2*4)/(4*4) = 8/16
So, 12/14 is not equal to 8/20
iii. 16/40
Divide the numerator and denominator with 2
That is, (16÷2)/(40÷2) = 8/20
iv. 40/100
Divide the numerator and denominator with 5
That is (40÷5)/(100÷5) = 8/20
Question 4.
The graph shows the money that Marco earns for different numbers of days worked. How much money does he earn per day?

$ _____
Answer:
$80
Explanation:
Total number of days worked = 7
Total earned money = 560 dollars
560 / 7 = 80 dollars per day
Question 5.
Megan answered 18 questions correctly on a test. That is 75% of the total number of questions. How many questions were on the test?
_____ questions
Answer:
24 questions
Explanation:
Megan answered 18 questions correctly
That is 75% of the total number of questions = 18
Then, 100% of the questions = 18*100/75 = 24
So, the total number of questions on the test = 24 questions
Share and Show – Page No. 343
Question 1.
Mariana runs at a rate of 180 meters per minute. How far does she run in 5 minutes?
_____ meters
Answer:
900 meters
Explanation:
Mariana runs at a rate of 180 meters per minute
Then, Mariana runs per 5 minutes = 5×180 = 900 meters
So, Mariana runs 900 meters per 5 minutes
Question 2.
What if Mariana runs for 20 minutes at the same speed? How many kilometers will she run?
_____ kilometers
Answer:
3.6 kilometers
Explanation:
From the given information
Marians runs at a rate of 180 meters per minute
Then the speed of Mariana = 180/1 = 180 meters per minute
If Mariana runs 20 minutes then the covered distance = 20×180 = 3600 meters
1000 meters = 1 kilometer
Then, 3600 meters = 3600/1000 = 3.6 kilometers
So, Mariana runs 3.6 kilometers in 20 minutes
Question 3.
A car traveled 130 miles in 2 hours. How fast did the car travel?
_____ miles per hour
Answer:
65 miles per hour
Explanation:
A car travelled 130 miles in 2 hours
Then the speed of the car = Distance/Time
That is, Speed of the car = 130 miles/ 2 hours = 65 miles per hour
So, the car travels 65 miles per hour
Question 4.
A subway car travels at a rate of 32 feet per second. How far does it travel in 16 seconds?
_____ feet
Answer:
512 feet
Explanation:
A subway car travels at a rate of 32 feet per second
1 second = 32 feet
then, 16 seconds = 16 x 32/1 = 512 feet
So, a subway car travels 512 feet per 16 seconds
Question 5.
A garden snail travels at a rate of 2.6 feet per minute. At this rate, how long will it take for the snail to travel 65 feet?
_____ minutes
Answer:
25 minutes
Explanation:
A garden snail travels at a rate of 2.6 feet per minute
So, 2.6 feet = 1 minute
Then, 65 feet = 65/2.6 = 650/26 = 25 minutes
So, the snail travels 65 feet in 25 minutes
Question 6.
A squirrel can run at a maximum speed of 12 miles per hour. At this rate, how many seconds will it take the squirrel to run 3 miles?
_____ seconds
Answer:
900 seconds
Explanation:
A squirrel can run at a maximum speed of 12 miles per hour
1 hour = 3600 seconds
So, the squirrel can run 12 miles in 3600 seconds
Then, the squirrel can run 3 miles in 3×3600/12 = 900 seconds
So, the squirrel can take 900 seconds of time to run 3 miles
Question 7.
A cyclist rides 8 miles in 32 minutes. What is the speed of the cyclist in miles per hour?
_____ miles per hour
Answer:
15 miles per hour
Explanation:
A cyclist rides 8 miles in 32 minutes
32minutes = 8 miles
Then, 60 minutes = 60×8/32 = 15 miles
So, a cyclist rides 15 miles in 60 minutes that is one hour
So, the speed of the cyclist per hour = 15 miles/ 1 = 15 miles per hour
Share and Show – Page No. 344
On Your Own
Question 8.
A pilot flies 441 kilometers in 31.5 minutes. What is the speed of the airplane?
_____ kilometers per minute
Answer:
14 kilometers per minute
Explanation:
From the given information
A pilot flies 441 kilometers in 31.5 minutes
Speed = Distance / Time
Here, distance = 441 kilometers
Time = 31.5 minutes
Speed of the airplane = 441/31.5 = 4410/315 = 14 kilometers per minute
Question 9.
Chris spent half of his money on a pair of headphones. Then he spent half of his remaining money on CDs. Finally, he spent his remaining $12.75 on a book. How much money did Chris have to begin with?
$ _____
Answer:
$51
Explanation:
Total money with the Chris= x amount
Chris spent half of his money on a pair of headphones = x/2
Then he spent half of his remaining money on CDs = x/4
Finally, he spent his remaining $12.75 on a book
So, total amount x = x/2+x/4+$12.75
$12.75 = (x-x/2-x/4)
= (4x-2x-x)/4
$12.75 = x/4
Then, x = $12.75×4 = $51
So, Chris have to begin with $51
Question 10.
André and Yazmeen leave at the same time and travel 75 miles to a fair. André drives 11 miles in 12 minutes. Yazmeen drives 26 miles in 24 minutes. If they continue at the same rates, who will arrive at the fair first? Explain.
____________
Answer:
André and Yazmeen leave at the same time and travel 75 miles to a fair
André drives 11 miles in 12 minutes
So, Andre can reach 75 miles in = 75×12/11
That is, Andre can travel 75 miles in 81 minutes
Yazmeen drives 26 miles in 24 minutes
So, Yazmeen can reach 75 miles in = 75×24/26 = 69 minutes
That means, Yazmeen can reach 75 miles in 69 minutes
So, Yazmeen can reach the fair first
Question 11.
Make Arguments Bonnie says that if she drives at an average rate of 40 miles per hour, it will take her about 2 hours to drive 20 miles across town. Does Bonnie’s statement make sense? Explain.
____________
Answer:
Make Arguments Bonnie says that if she drives at an average rate of 40 miles per hour, it will take her about 2 hours to drive 20 miles across town
Speed of the Bonnie = 40 miles per hour
Then, Bonnie can cover the distance in 2 hours = 2×40 = 80 miles
So, Bonnie statement is wrong
Question 12.
Claire says that if she runs at an average rate of 6 miles per hour, it will take her about 2 hours to run 18 miles. Do you agree or disagree with Claire? Use numbers and words to support your answer.
____________
Answer:
Claire says that if she runs at an average rate of 6 miles per hour, it will take her about 2 hours to run 18 miles
Claire runs in 1 hour = 6 miles
Then, Claire runs in 2 hours = 2×6 = 12 miles
So, the Claire statement is wrong
Problem Solving Distance, Rate, and Time Formulas – Page No. 345
Read each problem and solve.
Question 1.
A downhill skier is traveling at a rate of 0.5 mile per minute. How far will the skier travel in 18 minutes?
_____ miles
Answer:
9 miles
Explanation:
A downhill skier is traveling at a rate of 0.5 miles per minute
1 minute = 0.5 mile
then, 18 minutes = 18×0.5 = 9 miles
So, the skier travel 9 miles in 18 minutes
Question 2.
How long will it take a seal swimming at a speed of 8 miles per hour to travel 52 miles?
_____ hours
Answer:
6.5 hours
Explanation:
A seal swimming at a speed of 8 miles per hour
Then,52 miles = 52/8 = 6.5 hours
So, A seal swimming can travel 52 miles in 6.5 hours
Question 3.
A dragonfly traveled at a rate of 35 miles per hour for 2.5 hours. What distance did the dragonfly travel?
_____ miles
Answer:
87.5 miles
Explanation:
A dragonfly traveled at a rate of 35 miles per hour for 2.5 hours
That means, 1 hour = 35 miles
Then, 2.5 hours = 2.5×35 = 87.5 miles
So, a dragonfly travels 87.5 miles in 2.5 hours
Question 4.
A race car travels 1,212 kilometers in 4 hours. What is the car’s rate of speed?
_____ kilometers per hour
Answer:
303 kilometers per hour
Explanation:
A race car travels 1,212 kilometers in 4 hours
Speed = Distance/ Time
Here, distance = 1212 kilometers
Time = 4 hours
Then, Speed of the race car = 1212/4 = 303 kilometers per hour
Question 5.
Kim and Jay leave at the same time to travel 25 miles to the beach. Kim drives 9 miles in 12 minutes. Jay drives 10 miles in 15 minutes. If they both continue at the same rate, who will arrive at the beach first?
____________
Answer:
Kim reaches the beach first
Explanation:
Kim and Jay leave at the same time to travel 25 miles to the beach
Kim drives 9 miles in 12 minutes
Then, Kim travels 25 miles in = 25×12/9 = 33 minutes
Jay drives 10 miles in 15 minutes
Then, Jay travels 25 miles in = 25×15/10 = 37.5 minutes
So, Kim reaches the beach first
Question 6.
Describe the location of the variable d in the formulas involving rate, time, and distance.
Type below:
____________
Answer:
Formula Distance = Rate x Time
Distance (d) = Rate x Time
Lesson Check – Page No. 346
Question 1.
Mark cycled 25 miles at a rate of 10 miles per hour. How long did it take Mark to cycle 25 miles?
_____ hours
Answer:
2.5 hours
Explanation:
Mark cycled 25 miles at a rate of 10 miles per hour
That means, 10 miles = 1 hour
Then, 25 miles = 25/10 =2.5 hours
So, Mark take 2.5 hours to cycle 25 miles
Question 2.
Joy ran 13 miles in 3 \(\frac{1}{4}\) hours. What was her average rate?
_____ miles per hour
Answer:
4 miles per hour
Explanation:
Joy ran 13 miles in 3 ¼ hours
3 ¼ = 13/4 = 3.25 hours
Then, the average rate of the Joy = 13/3.25 hours = 4 miles per hour
Spiral Review
Question 3.
Write two ratios that are equivalent to \(\frac{9}{12}\).
Type below:
____________
Answer:
3/4 and 18/24
Explanation:
Equivalent ratios of 9/12 is 3/4 and 18/24
Multiply the numerator and denominator of ¾ with 3
That is 3×3/4×3 = 9/12
Divide the numerator and denominator of 18/24 with 2
That is (18/2)/(24/2) = 9/12
Question 4.
In the Chang family’s budget, 0.6% of the expenses are for internet service. What fraction of the family’s expenses is for internet service? Write the fraction in simplest form.
\(\frac{□}{□}\)
Answer:
\(\frac{3}{500}\)
Explanation:
In the Chang family’s budget, 0.6% of the expenses are for internet service
That is 0.6% = 0.6/100 = 6/1000 = 3/500
So, 3/500 part of the family’s expenses is used for internet service
Question 5.
How many meters are equivalent to 357 centimeters?
_____ meters
Answer:
3.57 meters
Explanation:
357 ntimeters
100centimeters = 1 meter
Then, 357 centimeters = 357/100 = 3.57 meters
3.57 meters is equivalent to 357 centimeters
Question 6.
What is the product of the two quantities shown below?
\(\frac{60 \mathrm{mi}}{1 \mathrm{hr}}\) × 12 hr
_____ miles
Answer:
720 miles
Explanation:
60 mi/1hr x 12 hr
That is, 60 milesx12 = 720 miles
So, the equivalent quantity of 60mi/1hr x 12hr is 720 miles
Chapter 6 Review/Test – Page No. 347
Question 1.
A construction crew needs to remove 2.5 tons of river rock during the construction of new office buildings
The weight of the rocks is ____________ pounds
Answer:
The weight of the rocks is 5,000 pounds
Explanation:
A construction crew needs to remove 2.5 tons of river rock during the construction of new office buildings
1 Ton = 2000 pounds
Then, 2.5 Tons = 2.5×2000
= 25×200 = 5000 pounds
So, the weight of the rocks is 5000 pounds
Question 2.
Select the conversions that are equivalent to 10 yards. Mark all that apply
Options:
a. 20 feet
b. 240 inches
c. 30 feet
d. 360 inches
Answer:
c. 30 feet
d. 360 inches
Explanation:
a. 20 feet
3feet = 1 yard
Then, 20 feet = 20/3 yard
b. 240 inches
36 inches = 1 yard
Then, 240 inches = 240/36 = 6 yards
c. 30 feet
3feet = 1 yard
Then, 30 feet =30/3 = 10 yards
d. 360inches
36 inches = 1 yard
Then, 360 inches = 360/36 = 10 yards
So, 30 feet and 360 inches are equivalent to 10 yards
Question 3.
Meredith runs at a rate of 190 meters per minute. Use the formula d=r×t to find how far she runs in 6 minutes.
_____ meters
Answer:
1,140 meters
Explanation:
Meredith runs at a rate of 190 meters per minute
Formula d = r x t
Here, d= 190 meters, t = 1 minute
Then, r = 190/1 = 190 meters per minute
Now, t = 6 minutes and r = 190 meters per minute
Then d = 190 x 6 = 1,140 meters
Question 4.
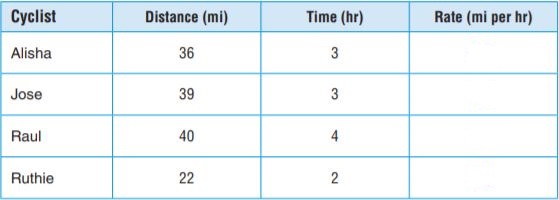
The table shows data for 4 cyclists during one day of training. Complete the table by finding the speed for each cyclist. Use the formula r = d ÷ t.
Type below:
____________
Answer:
D = RxT
Alisha
36 = Rx3
Then, Rate of Alisha =36/3 =12 miles per hour
Jose
39 = Rx3
Then, Rate of Jose = 39/3 = 13 miles per hour
Raul
40 = Rx4
Then, Rate of Raul = 40/4 = 10 miles per hour
Ruthie
22= Rx2
Then, Rate of Ruthie = 22/2 = 11 miles per hour
Page No. 348
Question 5.
For numbers 5a–5c, choose <, >, or =.
5a. 5 kilometers Ο 5,000 meters
5b. 254 centiliters Ο 25.4 liters
5c. 6 kilogram Ο 600 gram
5 kilometers _____ 5,000 meters
254 centiliters _____ 25.4 liters
6 kilogram _____ 600 gram
Answer:
5a. 5 kilometers Ο 5,000 meters
5b. 254 centiliters Ο 25.4 liters
5c. 6 kilogram Ο 600 gram
5 kilometers = 5,000 meters
254 centiliters < 25.4 liters
6 kilogram > 600 gram
Explanation:
a. 5 kilometers —— 5000 meters
1 kilometer = 1000 meters
then,5 kilometers 5×1000 = 5000 meters
So, 5 kilometers = 5000 meters
b. 254 centiliters ——25.4 liters
100centiliters = 1 liter
Then, 254 centiliters = 254/100 = 2.54 liters
So, 254 centiliters < 25.4 liters
c. 6 kilograms —– 600 grams
1kilogram = 1000 grams
Then, 6 kilograms = 6000 grams
So, 6 kilograms > 600 grams
Question 6.
A recipe calls for 16 fluid ounces of light whipping cream. If Anthony has 1 pint of whipping cream in his refrigerator, does he have enough for the recipe? Explain your answer using numbers and words.
____________
Answer:
A recipe calls for 16 fluid ounces of light whipping cream
8 fluid ounces = 1 cup
So, 16 fluid ounces = 2 cups = 1 pint
If Anthony has 1 pint of whipping cream in his refrigerator, then it is enough for the recipe
Question 7.
For numbers 7a–7d, choose <, >, or =.
7a. 43 feet Ο 15 yards
7b. 10 pints Ο 5 quarts
7c. 5 tons Ο 5,000 pounds
7d. 6 miles Ο 600 yards
43 feet _____ 15 yards
10 pints _____ 5 quarts
5 tons _____ 5,000 pounds
6 miles _____ 600 yards
Answer:
43 feet < 15 yards
10 pints = 5 quarts
5 tons > 5,000 pounds
6 miles > 600 yards
Explanation:
a. 43 feet —- 15 yards
3feet = 1 yard
Then, 43 feet = 43/3 = 14.3 yards
So, 43 feet < 15 yards
b. 10 pints —- 5 quarts
1 pints = 1 quart
then, 10 pints = 10/2 = 5 quarts
So, 10 pints = 5 quarts
c. 5 tons —– 5000 pounds
1 ton = 2000 pounds
then, 5 tons = 5×2000 = 10,000 pounds
So, 5 tons > 5000 pounds
d. 6 miles —- 600 yards
1 mile =1760 yards
then, 6 miles = 6×1760 = 10,560yards
So, 6 miles > 600 yards
Question 8.
The distance from Caleb’s house to the school is 1.5 miles, and the distance from Ashlee’s house to the school is 3,520 feet. Who lives closer to the school, Caleb or Ashlee? Use numbers and words to support your answer.
____________
Answer:
There are 5280 feet in one mile.
So, you need to change the miles to feet.
1.5 x 5280 = 7920.
7920 > 3520
So, Ashley lives closer.
Page No. 349
Question 9.
Write the mass measurements in order from least to greatest.

Type below:
____________
Answer:
7.4 kilograms, 7.4 centigrams, 7.4 decigrams
Question 10.
An elephant’s heart beats 28 times per minute. Complete the product to find how many times its heart beats in 30 minutes

Type below:
____________
Answer:
840 beats
Explanation:
An elephant’s heart beats 28 times per minute
Then, elephant’s heart beats in 30 minutes = 28 x 30 = 840
So, an elephant’s heartbeat is 840 times in 30 minutes
Question 11.
The length of a rectangular football field, including both end zones, is 120 yards. The area of the field is 57,600 square feet. For numbers 11a–11d, select True or False for each statement.
11a. The width of the field is 480 yards.
11b. The length of the field is 360 feet.
11c. The width of the field is 160 feet.
11d. The area of the field is 6,400 square yards.
11a. ____________
11b. ____________
11c. ____________
11d. ____________
Answer:
11a. True
11b. True
11c. False
11d. False
Explanation:
The length of a rectangular football field, including both end zones, is 120 yards
The area of the field is 57,600 square feet
That is length x width = 57,600 square feet
Here, length = 120 yards
Then, width = 57,600/120 = 480 yards
11a. True
11b. 1 yard = 3 feet
Then, 120 yards = 120×3 = 360 feet
True
11c. 480 yards = 480×3 = 1440
False
11d. 6400 square yards
3 feet = 1 yard
then, 57,600 square feet = 57,600/3 = 19,200 square yards
False
Question 12.
Harry received a package for his birthday. The package weighed 357,000 centigrams. Select the conversions that are equivalent to 357,000 centigrams. Mark all that apply.
Options:
a. 3.57 kilograms
b. 357 dekagrams
c. 3,570 grams
d. 3,570,000 decigrams
Answer:
a. 3.57 kilograms
b. 357 dekagrams
c. 3,570 grams
Explanation:
Harry received a package for his birthday
The package weighed 357,000 centigrams
100centigrams = 1 gram
Then, 357,000 centigrams = 357,000/100 = 3570 grams
1000 grams = 1 kilogram
Then, 3570 grams = 3570/1000 = 3.57 kilograms
10grams = 1 dekagram
Then, 3570 grams = 3570/10 = 357 dekagrams
1gram = 10 decigrams
Then, 3570 grams = 35700 decigrams
Options a, b and c are true
Page No. 350
Question 13.
Mr. Martin wrote the following problem on the board.
Juanita’s car has a gas mileage of 21 miles per gallon. How many miles can Juanita travel on 7 gallons of gas?
Alex used the expression \(\frac{21 \text { miles }}{\text { 1 gallon }} \times \frac{1}{7 \text { gallons }}\) to find the answer. Explain Alex’s mistake.
Type below:
____________
Answer:
Juanita’s car has a gas mileage of 21 miles per gallon
Juanita traveled miles on 7 gallons of gas = 21×7 = 147 miles
But, Alex used the expression 21 miles 1 gallon ×17 gallons
In the place of 7 gallons, Alex used 17 gallons
Question 14.
Mr. Chen filled his son’s wading pool with 20 gallons of water.
20 gallons is equivalent to ____________ quarts.
Answer:
80 quarts
Explanation:
Mr. Chen filled his son’s wading pool with 20 gallons of water
1gallon = 4 quarts
Then, 20 gallons = 20×4 = 80 quarts
So, 20 gallons is equivalent to 80 quarts
Question 15.
Nadia has a can of vegetables with a mass of 411 grams. Write equivalent conversions in the correct boxes.

Type below:
____________
Answer:
0.411, 41.1, 4.11
Explanation:
Nadia has a can of vegetables with a mass of 411 grams
1000 grams = 1 kilogram
Then, 411 grams = 411/1000 = 0.411 kilograms
100grams = 1 hectogram
Then, 411 grams = 411/100 = 4.11 hectograms
10grams = 1 dekagram
Then, 411 grams = 411/10 = 41.1 dekagram
Question 16.
Steve is driving 440 miles to visit the Grand Canyon. He drives at an average rate of 55 miles per hour. Explain how you can find the amount of time it will take Steve to get to the Grand Canyon.
Type below:
____________
Answer:
Steve is driving 440 miles to visit the Grand Canyon
He drives at an average rate of 55 miles per hour
Then, 440 miles = 440/55 = 8 hours
So, Steve can take 8 hours of time to visit the Grand Canyon
Page No. 351
Question 17.
Lucy walks one time around the lake. She walks for 1.5 hours at an average rate of 3 miles per hour. What is the distance, in miles, around the lake?
_____ miles
Answer:
4.5 miles
Explanation:
Lucy walks one time around the lake
She walks for 1.5 hours at an average rate of 3 miles per hour
1 hour = 3 miles
Then, 1.5 hours = 1.5×3 = 4.5 miles
So, Luke walks 4.5 miles around the lake
Question 18.
The parking lot at a store has a width of 20 yards 2 feet and a length of 30 yards.

Part A
Derrick says that the width could also be written as 22 feet. Explain whether you agree or disagree with Derrick.
Type below:
____________
Answer:
Derrick says that the width could also be written as 22 feet
1yard = 3 feet
20 yards = 60 feet
So, we cannot write 20 yards 2 feet as 22 feet
Question 19.
Part B
The cost to repave the parking lot is $2 per square foot. Explain how much it would cost to repave the parking lot.
Type below:
____________
Answer:
The cost to repave the parking lot is $2 per square foot
Parking lot area =20 yards 2 feet x 30 yards
1yard = 3 feet
Then, 20 yards = 20×3 = 60 feet
30 yards = 30×3 = 90 feet
so, Parking lot area = 62 feet x 90 feet = 5580 feet
1 square foot cost = $2
then, 5580 feet cost = 2×5580 = $11,160
Page No. 352
Question 19.
Jake is using a horse trailer to take his horses to his new ranch.
Part A
Complete the table by finding the weight, in pounds, of Jake’s horse trailer and each horse.
Type below:
____________
Answer:
Horse weight in Tons = 0.5 T
Trailer weight in Tons = 1.25 T
1 ton = 2000 pounds
then, 0.5 T = 0.5×2000 = 1000 pounds
then, 1.25 T = 1.25×2000 = 2,500 pounds
Question 19.
Part B
Jake’s truck can tow a maximum weight of 5,000 pounds. What is the maximum number of horses he can take in his trailer at one time without going over the maximum weight his truck can tow? Use numbers and words to support your answer.
Type below:
____________
Answer:
Max. No of Horses = (Max weight truck can tow)/(Average weight of one horse)
The weight of a horse is not given in the question .Thus, we assume the average weight of one horse, to be equal to 1000 pounds,
Max. No of Horses = 5000 pounds/ 1000 pounds
Max. No of Horses = 5
Question 20.
A rectangular room measures 13 feet by 132 inches. Tonya said the area of the room is 1,716 square feet. Explain her mistake, then find the area in square feet.
Type below:
____________
Answer:
A rectangular room measures 13 feet by 132 inches =13 feetx132 inches
Tonya said the area of the room is 1,716 square feet
Area of the rectangular room = 13 feet x 132 inches
12inches = 1 foot
Then, 132 inches = 132/12 = 11 feet
So, the area of the rectangular room = 13 feet x 12 feet = 156 feet
So, Tonya’s answer is wrong
Conclusion:
Go Math Grade 6 Answer Key Chapter 6 Convert Units of Length is free online. Get your Go Math Grade 6 Solution Key and start practice. To get the best way of learning and to score high marks in the exam, the only way to learn maths is by using Go Math Grade 6 Chapter 6 Convert Units of Length Answer Key.
Go Math Grade 6 Answer Key Chapter 6 Convert Units of Length Read More »














































































































































































































 img 14
img 14